Definición de Teorema

Ángel Zamora Ramírez
Licenciado en Física

Un teorema es una afirmación o proposición matemática que es demostrada de manera rigurosa y que es verdadera en un contexto específico. Los teoremas parten de axiomas o de otros teoremas que ya han sido demostrados.

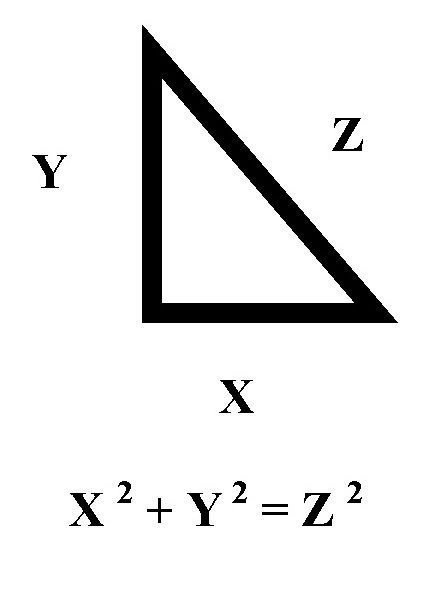Se suele pensar en las matemáticas como esta disciplina que se encarga de estudiar los números y de hacer cálculos con ellos. No obstante, las matemáticas son mucho más que eso. La labor matemática es un constante proceso que mezcla la lógica y la creatividad, y muchas veces esto conlleva al establecimiento de principios que son verdaderos en un contexto matemático bien definido. Los teoremas son la culminación de este proceso y son uno de los pilares más importantes de las matemáticas. La proposición de un teorema y su demostración requieren de un largo estudio y muchos de ellos han tomado cientos de años para ser demostrados.

Aclaraciones sobre la terminología de afirmaciones/proposiciones en matemáticas

En las matemáticas existen diversos tipos de afirmaciones o proposiciones que parten o no de un teorema ya establecido. Hay ocasiones en que algunos de estos términos se utilizan como sinónimo de teorema, lo cual, además de ser erróneo, puede llevar a ciertas confusiones al respecto. Los distintos tipos de afirmaciones o proposiciones que existen son los siguientes:

– Axioma: Un axioma es una proposición o enunciado que resulta tan evidente que no requiere de una demostración matemática. Un ejemplo de axioma es el siguiente: Si se tiene un punto A y un punto B en un espacio plano, la distancia más corta entre ellos es una línea recta. En este caso resulta evidente que ese enunciado es cierto ya que la línea recta es menor a cualquier trayectoria que se pueda trazar entre el punto A y el punto B. Los axiomas muchas veces son la base de distintas áreas de las matemáticas y de ellos surgen muchos teoremas.

– Lema: Un lema es una proposición que forma parte de un teorema más general. Al igual que los teoremas, los lemas también se someten a una demostración rigurosa. A pesar de que los lemas suelen considerarse como “teoremas menores”, muchos de estos han llegado a considerarse teoremas en sí mismo debido a la importancia que suponen.

– Corolario: Un corolario es una proposición o afirmación que surge inmediatamente de un teorema. Supone una consecuencia obvia de un teorema y generalmente no requiere de una demostración matemática.

– Proposición: Una proposición es un enunciado que no parte de ningún teorema en particular y que a priori no puede considerarse como verdadero o como falso. La demostración de proposiciones muchas veces lleva al establecimiento de teoremas.

– Conjetura: Una conjetura es una afirmación o proposición que se considera como verdadera pero que no ha sido demostrada o refutada. Una vez que se demuestra la veracidad de una conjetura esta pasa a ser un teorema.

Un ejemplo: El Teorema de Pitágoras

Quizá el teorema más famoso de las matemáticas es el Teorema de Pitágoras, pero además de su fama, este teorema es uno de los más importantes. El Teorema de Pitágoras lo podemos encontrar en muchas áreas de las matemáticas como la Trigonometría, la Geometría y el Cálculo. Además, también forma parte fundamental de otras áreas como la Física, la Astronomía, las Ingenierías, etc.

Este célebre teorema es válido para cualquier triángulo rectángulo. Un triángulo rectángulo es aquel en el que uno de los ángulos que lo forman es un ángulo recto, es decir, un ángulo de 90°. A los lados que forman este ángulo recto se les llama “catetos” y el lado restante se denomina “hipotenusa”.

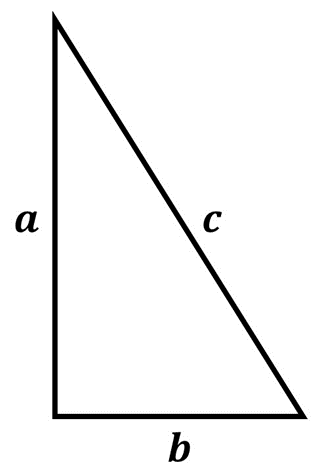
El Teorema de Pitágoras establece que dado un triángulo rectángulo con catetos \(a\) y \(b\) e hipotenusa \(c\), se satisface que:

\({c^2} = {a^2} + {b^2}\)

Expresándolo con palabras: La suma del cuadrado de los catetos es igual al cuadrado de la hipotenusa. No obstante, este enunciado no surge de la nada y se ha demostrado de mil y un formas que es correcto. A continuación, procederemos a demostrarlo.

Demostración

Consideremos un triángulo rectángulo cualquiera con catetos \(a\) y \(b\) e hipotenusa \(c\), tal y como el presentado anteriormente. Vamos a tomar tres triángulos más idénticos a este para formar un cuadrado de la siguiente manera.

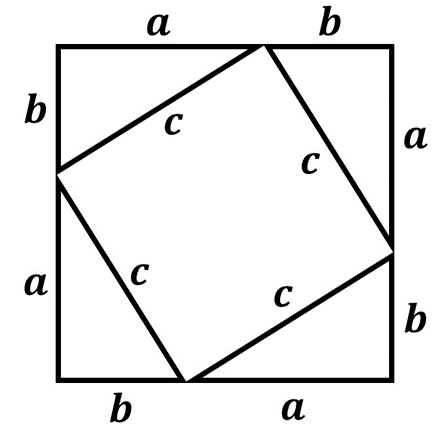
Ahora procederemos a calcular el área de este cuadrado que formamos con los cuatro triángulos rectángulos. Hay dos formas en las que nosotros podemos calcular el área del cuadrado. La primera es simplemente darnos cuenta que la medida de los lados de este cuadrado que formamos es \(a + b\), es decir, la suma de los catetos. Por lo tanto, el área del cuadrado según este método será simplemente:

\({A_1} = {\left( {a + b} \right)^2}\)

La segunda manera en la que podemos calcular el área del cuadrado es considerando que este cuadrado se conforma de los cuatro triángulos rectángulos que utilizamos y de un cuadrado más pequeño cuyos lados miden \(c\) y que se conforma de las hipotenusas de los triángulos. El área del cuadrado será entonces la suma de las áreas de los cuatro triángulos y del área del cuadrado más pequeño.

El área de cada triángulo rectángulo es igual a \(ab/2\) y el área del cuadrado es igual a \({c^2}\). Por lo tanto, el área del cuadrado en este caso estará dada por:

\({A_2} = 4\left( {\frac{{ab}}{2}} \right) + {c^2}\)

Lo cual nos da como resultado:

\({A_2} = 2ab + {c^2}\)

Al tratarse del mismo cuadrado ambas áreas que hemos obtenido tienen que ser igual, es decir, que \({A_1} = {A_2}\). Igualando ambas expresiones se tiene que:

\(2ab + {c^2} = {\left( {a + b} \right)^2}\)

Desarrollando el binomio al cuadrado del lado derecho de la ecuación obtenemos que:

\(2ab + {c^2} = {a^2} + 2ab + {c^2}\)

Podemos darnos cuenta que el término \(2ab\) aparece en ambos lados de la ecuación, por lo tanto, al despejarlo de un lado se cancela y finalmente se llega a que:

\({c^2} = {a^2} + {b^2}\)

Lo cuál es precisamente lo expresado por el Teorema de Pitágoras y de esta manera queda demostrado.

Este es sólo un ejemplo de cómo es que se demuestra matemáticamente que una proposición o enunciado matemático es verdadero y de esta manera se formula un Teorema que es verídico en el ámbito en el que se plantea.

Por: Ángel Zamora Ramírez. Licenciado en Física egresado de la Universidad de Colima. Maestro en Ciencias en Ingeniería y Física Biomédicas egresado del CINVESTAV. Amante de la divulgación científica.

Art. actualizado: Oct. 2023; sobre el original de enero, 2009.

Datos para citar en modelo APA: Zamora Ramírez, A. (Oct. 2023). Definición de Teorema. DefiniciónABC. Desde https://www.definicionabc.com/general/teorema.php