Definición de Fracción

Maestría en Matemáticas, Dr. en Ciencias
Las fracciones además de representarse como el cociente de dos enteros, éstas pueden representarse como porcentaje, de manera gráfica y verbal. En las posteriores 6 aplicaciones mostraremos cómo pueden usarse para resolver diferentes problemas.
Aplicación/ejemplo 1: David y Antonia comieron pizzas con sus papás; la pizza de David es la de la izquierda y la de Antonia la de la derecha, ¿quién comió más?

Respuesta: La pizza de David se cortó en 3 partes iguales (en tercios) y se comió dos de ellas y la de Antonia en cinco partes iguales (en quintos) y se comió 3, por lo cual debemos averiguar cuál de estas fracciones es mayor \(\frac{2}{3},\;\frac{3}{5}.\) Para poder comparar las fracciones anteriores, las llevaremos a fracciones equivalentes que tengan un denominador común:
\(\frac{2}{3} = \frac{{2\left( 5 \right)}}{{3\left( 5 \right)}} = \frac{{10}}{{15}}\)\(\frac{3}{5} = \frac{{3\left( 3 \right)}}{{5\left( 3 \right)}} = \frac{9}{{15}}\)
Con la conversión anterior ya es fácil determinar que \(\frac{2}{3} > \frac{3}{5}\) por lo cual David comió más pizza y aún más; podemos afirmar que comió \(\frac{1}{{15}}\) más que su hermana.
Aplicación/ejemplo 2: La sangre del ser humano se clasifica en grupos debido a que presenta características diferentes. Los grupos de sangre son: A, B, AB y O; a su vez son clasificadas en positivo y negativo.
La siguiente tabla muestra cómo se distribuyen a nivel mundial los grupos sanguíneos del ser humano.
| A | B | AB | O |
|---|---|---|---|
| 21 de cada 50 | 2 de cada 25 | 1 de cada 25 | 23 de cada 50 |
¿La información es numéricamente coherente? Respuesta:
La tabla anterior también la podemos presentar como
| A | B | AB | O |
|---|---|---|---|
| 21 de cada 50 | 4 de cada 50 | 2 de cada 50 | 23 de cada 50 |
Notemos que: 21+4+2+23=50 por lo cual podemos afirmar que la información es numéricamente coherente.
Hemos encontrado una manera alternativa para comprobar el siguiente hecho:
\(\frac{{21}}{{50}} + \frac{2}{{25}} + \frac{1}{{25}} + \frac{{23}}{{50}} = \frac{{21}}{{50}} + \frac{4}{{50}} + \frac{2}{{50}} + \frac{{23}}{{50}} = \frac{{50}}{{50}} = 1\)
La siguiente tabla muestra como se distribuyen en la Ciudad de México los grupos sanguíneos del ser humano.
| A | B | AB | O |
|---|---|---|---|
| 1 de cada 4 | 17 de cada 200 | 3 de cada 200 | 13 de cada 20 |
¿La información es numéricamente coherente? ¿El tipo de sangre B es dónde es más común en la Ciudad de México o a nivel mundial? ¿Qué sucede en los demás casos?
Respuestas
Para la primera respuesta presentaremos la tabla de la siguiente manera:
| A | B | AB | O |
|---|---|---|---|
| 50 de cada 200 | 17 de cada 200 | 3 de cada 200 | 130 de cada 200 |
Al sumar: 50+17+3+130=200, ya podemos garantizar que la información es numéricamente coherente.
Para responder a la segunda respuesta presentaremos la información de la tabla como sigue:
| Tipo de Sangre | Nivel Mundial | Ciudad de México |
|---|---|---|
| A | 42 de cada 100 | 25 de cada 100 |
| B | 16 de cada 200 | 17 de cada 200 |
| AB | 8 de cada 200 | 3 de cada 200 |
| O | 46 de cada 100 | 65 de cada 100 |
Con la información presentada de tal manera podemos afirmar que la sangre tipo B es más común en la Ciudad de México que a Nivel Mundial, es decir:
\(\frac{{17}}{{200}} > \frac{4}{{50}}\)
De forma similar se resuelven los demás casos.
Aplicación 3: Una cubeta grande de miel tiene 19 litros, ¿cuántas botellas de \(\frac{3}{4}\) de litro se pueden llenar con la miel de la cubeta?, ¿cuánta miel sobra?
Respuesta
Se deben repartir 19 litros en botellas, de \(\frac{3}{4}\) de litro, para saber cuántas botellas se van a llenar es necesario realizar una división:
\(19 \div \frac{3}{4} = \frac{{19}}{1} \div \frac{3}{4} = \frac{{19\left( 4 \right)}}{3} = \frac{{76}}{3} = \frac{{75 + 1}}{3} = \frac{{75}}{3} + \frac{1}{3} = 25 + \frac{1}{3}\)
Interpretación
Al efectuar la división se ha obtenido una fracción mixta: \(25\frac{1}{3}\).
Es decir, se van a llenar 25 botellas de \(\frac{3}{4}\) de litro con los 19 litros de miel.
Para saber cuánta miel va a sobrar recordaremos lo siguiente:
Si \(a \div b = c,\) entonces \(a = bc\); en nuestro caso concreto:
\(19 = \left( {25 + \frac{1}{3}} \right)\frac{3}{4}\)\(19 = 25\left( {\frac{3}{4}} \right) + \frac{1}{3}\left( {\frac{3}{4}} \right)\)
Lo anterior nos indica que sobra un tercio de una botella de \(\frac{3}{4}\), es decir, \(\frac{1}{4}\) de miel.
Hay otra manera de resolverlo.
Cada litro de miel equivale a 4 botellas de \(\frac{1}{4}\), de miel así que 19 botellas de miel llenan \(19 \times 4 = 76\) botellas de miel, cada 3 botellas de miel equivalen a una botella de \(\frac{1}{4}\) de miel como:
\(75 = 25 \times 3 + 1\)podemos concluir que se van a llenar 25 botellas de \(\frac{3}{4}\) de miel y sobra una botella de \(\frac{1}{4}\) de miel.
Aplicación 4: Las ventas de una empresa durante el año 2021 se redujeron 20% comparadas con su desempeño en el 2020. ¿A qué tasa debe aumentar sus ventas durante el 2022 con respecto al 2021, para recuperar el nivel que se tenían en 2020?
Respuesta: Un 20% equivale a \(\frac{1}{5}\) del todo y lo representaremos en el siguiente gráfico:
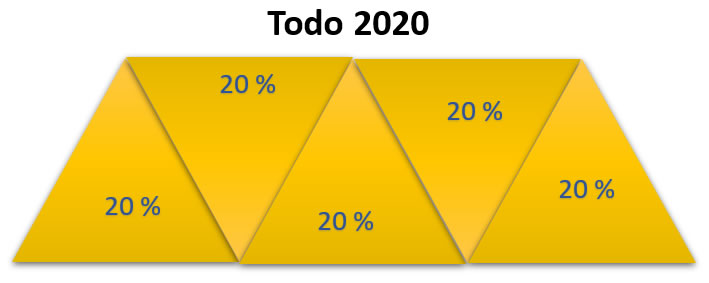
En el 2021 se perdió un 20%, con respecto al 2020, es decir se perdió un triángulo, el cual queda representado como:

Ahora cada triángulo representa un 25% del todo en el 2021
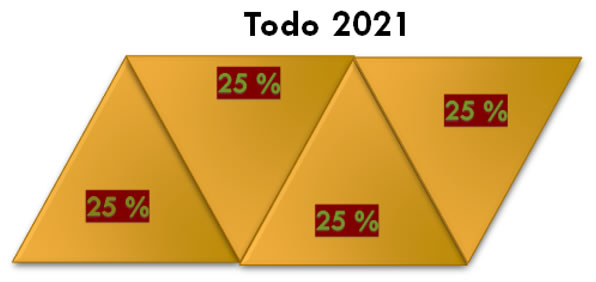
Así que para llegar al nivel de ventas se debe de aumentar un 25% de ventas que se hicieron en el 2021.
Aplicación 5: Al comprar un par de tenis, una persona pagó $420.00; si el par tenía un 25% de descuento, ¿cuál era su precio original?
Respuesta: Un 25% representa un \(\frac{1}{4}\) del todo, como lo indica la figura siguiente:
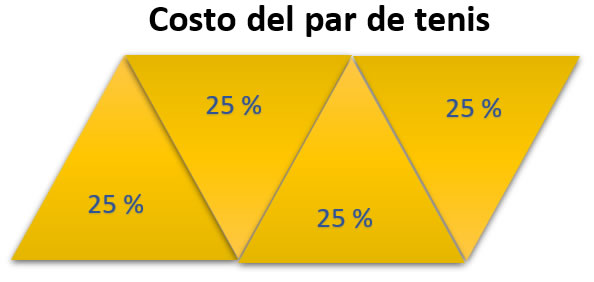
Al quitar un triángulo nos queda:

Ahora cada triángulo representa un tercio de $420, es decir, $140.

Finalmente podemos concluir que el costo original de los tenis era: \(4 \times 140 = 560\)
Aplicación 6: Un hombre que iba por el camino vio a un grupo de personas que iban hacía él y les dijo: “Si viniera otro grupo de su tamaño y se añadiese la mitad de otro grupo como el de ustedes y después se añadiese la mitad de este número, entonces conmigo seríamos cien.” ¿Cuántos hombres forman el caminante?
Respuesta:

Para resolverlo usaremos el siguiente esquema:

Representa al grupo de hombres.
De acuerdo con el texto se obtiene el siguiente esquema
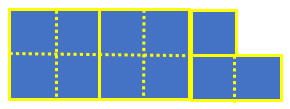
El cual se puede dividir de la siguiente manera
El esquema anterior representa a 99 hombres y hay 11

por lo cual representa a 9.
En conclusión, el hombre vio a 36 personas.

Art. actualizado: Nov. 2022; sobre el original de febrero, 2012.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.