Definición de Cuadrilátero

Ingeniera Industrial, MSc en Física, y EdD
El término cuadrilátero, por el latín quadrilaterus, remite a que “tiene cuatro lados”, razón por la cual en la geometría euclidiana se define como figura geométrica compuesta por cuatro lados: cuatro ángulos internos y cuatro vértices. Los cuadriláteros, también se conocen como cuadrángulos o tetrágonos, poseen un sinnúmero de aplicaciones en casi cualquier área del conocimiento, ya que se emplean en diseños, construcciones civiles, representación de enlaces químicos, entre otros.
Elementos de los cuadriláteros
Independientemente del tipo de cuadrilátero, siempre estará conformado por las siguientes características:
• Cuatro lados, cuatro ángulos internos y cuatro vértices.
• Dos diagonales que atraviesan la figura desde una esquina a otra y dividen el cuadrilátero en cuatro triángulos.
• La región interna delimitada por sus cuatro lados forma un área.
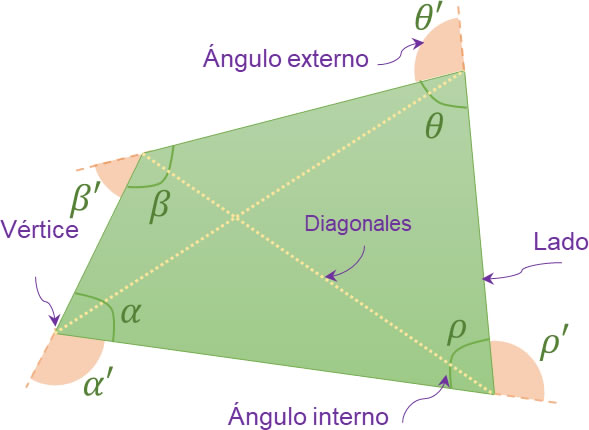
La figura señala los elementos constitutivos de los cuadriláteros
Clasificación de los cuadriláteros
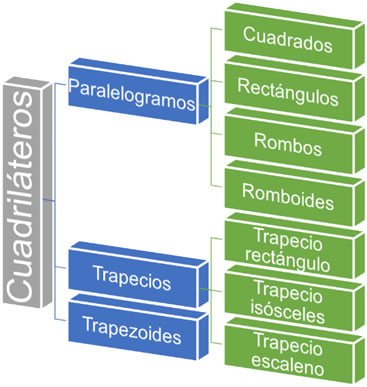
Esquema que muestra la clasificación de los cuadriláteros según la disposición de sus lados.
Los cuadriláteros se pueden dividir en tres categorías, las cuales a su vez se pueden subdividir en otras categorías, cuyas características se describen a continuación:
• Paralelogramos: se denominan así porque poseen dos pares de lados paralelos. Se clasifican en:
o Cuadrado: esta figura posee sus cuatro lados de igual longitud y sus cuatro ángulos internos son rectos (90°). Los cuadrados tienen ejes de simetría horizontal, vertical y sus diagonales.
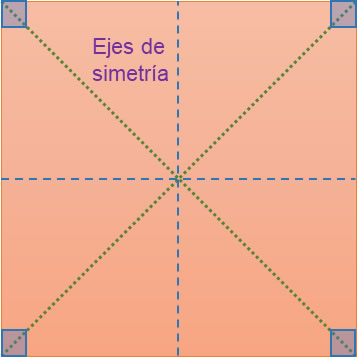
Las líneas segmentadas representan los ejes de simetría del cuadrado, y el punto de intersección de estas líneas representa su centro geométrico o centroide de área.
o Rectángulo: este cuadrilátero se caracteriza por tener dos pares de lados de igual longitud. Los lados contiguos son desiguales y al igual que los cuadrados, poseen cuatro ángulos internos de 90°.

Muchos objetos de uso cotidiano tienen forma rectangular, como las hojas de los cuadernos, la pantalla y teclado de un computador portátil o la pantalla de un teléfono celular.
Rombo: al igual que los cuadrados, este cuadrilátero posee sus cuatro lados con la misma longitud paralelos dos a dos, pero sus ángulos internos opuestos son iguales, dos agudos (menores de 90°) y dos obtusos (mayores de 90°).

Esta señal de tránsito indica que circulan vehículos en ambos sentidos y su contorno está formado por un rombo.
Romboide: posee lados y ángulos opuestos iguales dos a dos. Sus lados contiguos son diferentes. Al igual que los rombos, tienen dos agudos (menores de 90°) y dos obtusos (mayores de 90°).

Esta estrella simétrica de seis puntas se forma mediante el arreglo de seis romboides que se tocan en uno de sus vértices.
• Trapecios: estas figuras tienen dos lados paralelos entre sí pero con diferente longitud, y dos lados no paralelos. Los lados paralelos se denominan base mayor y base menor en función de sus dimensiones. Los trapecios se clasifican a su vez en:
o Trapecio rectángulo: este trapecio debe su nombre a dos de sus ángulos internos son rectos (iguales a 90°). Los otros ángulos son uno agudo (< 90°) y el otro obtuso (> 90°).

El trapecio de la imagen es de tipo rectángulo. Se observan dos ángulos internos de 90° y dos lados opuestos paralelos llamados base, en este caso, la base menor es el lado superior y la mayor es el lado inferior.
o Trapecio isósceles: este trapecio posee un eje de simetría, ya que tiene sus dos lados no paralelos con la misma medida.
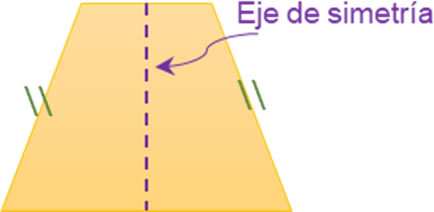
El trapecio isósceles que se muestra posee sus lados laterales con la misma longitud, su eje de simetría es la línea vertical segmentada.
o Trapecio escaleno: este trapecio no posee simetría, ya que ninguno de sus lados tiene la misma longitud. Además, se diferencia del trapecio rectángulo porque ninguno de sus ángulos es recto.

El adjetivo escaleno se emplea en las figuras geométricas para expresar que todos los lados son desiguales, como el caso del trapecio escaleno que se muestra.
Trapezoides: estas figuras no tienen sub-clasificación, y aquí se agrupan aquellos cuadriláteros que no poseen lados ni ángulos iguales.
El contorno de la cometa, papalote o papagayo posee una forma de trapezoide, ya que ni sus lados, ni sus ángulos internos son iguales.
Áreas y perímetros de los cuadriláteros

En el boxeo y otros deportes de combates, al área acordonada donde se desarrolla la lucha se le denomina cuadrilátero porque es una región cerrada delimitada por cuatro lados.
Perímetro: En todas las figuras, el perímetro se determina con la suma de sus lados. Si se denomina l1, l2, l3 y l4 a cada uno de los lados de un cuadrilátero, su perímetro (P) se determina mediante la expresión:
\(P = {l_1} + {l_2} + {l_3} + {l_4}\)
Las unidades del perímetro deben corresponder con la dimensión longitud, por ejemplo, metros (m), centímetros (cm), pulgadas (pulg), etc.
Área: En el caso de las áreas de los cuadrados y rectángulos, se determina multiplicando la base (b) por la altura (h):

\(A = b \cdot h\)
Para los trapecios, el área se determina con la semi-suma de sus bases multiplicada por su altura:
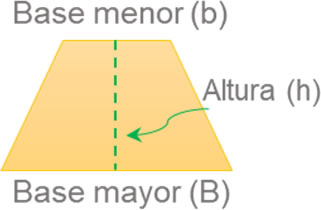
\(A = \left( {\frac{{b + B}}{2}} \right) \cdot h\)
Para el caso de los rombos y romboides, el área se halla multiplicando sus diagonales divididas entre dos:
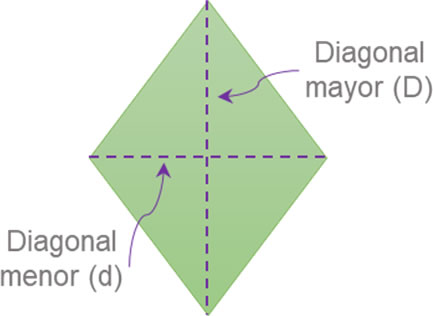
\(A = \frac{{D \cdot d}}{2}\)
En los trapezoides, el área se debe determinar dividiéndolo en otras figuras más simples, por ejemplo, en dos triángulos. Se determina el área de cada una de las figuras que lo componen y luego se suman:
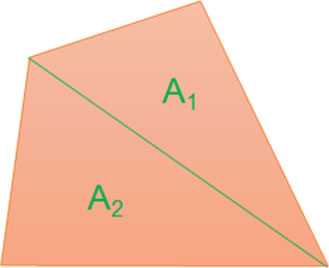
\(A = \sum {A_i}\)
Nota: la dimensión de un área debe ser de longitud al cuadrado, por ejemplo, metros cuadrados (m2).

Art. actualizado: Dic. 2022; sobre el original de agosto, 2015.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.