Definición de Volumen

Ingeniera Industrial, MSc en Física, y EdD
1. El volumen puede definirse de manera simple como el tamaño o la extensión de algo. Término muy utilizado en la vida cotidiana así como en diversas áreas como la geometría, la física y la bibliografía. Ejemplos: a) ‘recibí un gran volumen de tareas para esta semana’; b) ‘el caudal del río está bajando mucho este invierno’.
2. En referencia al sonido, el volumen se refiere a su nivel de intensidad, en los extremos alto y bajo, que dependiendo del caso permite su manipulación. Ejemplo: ‘Subí el volumen de la televisión para que todos pudieran escuchar las noticias’.
3. Bibliología. En una obra o periódico, el volumen equivale a una parte impresa individual y que tiene relación con la publicación en cuanto parte constituyente de la misma, ya sea a modo de continuación (ej., ‘una obra de 10 volúmenes’) o en función de un orden cronológico (ej., ‘volumen 01 del año 2000’).
4. Física/geometría. Extensión de las tres dimensiones -alto+ancho+largo- de un cuerpo, o sea, el volumen es el espacio ocupado por un elemento cuantificado en metros cúbicos (m³).
Etimología: Por el latín volūmen, en cuanto ‘rollo’, vinculado al manejo de papiros, manuscritos, asociado al verbo volvĕre, de ‘enrollar’, y que remite a la palabra ‘volver’.
Cat. gramatical: Sustantivo masc.
En sílabas: vo-lu-men.
Volumen (en Física)
El volumen es una cantidad física escalar que expresa el espacio tridimensional ocupado por un cuerpo. Se trata de una cantidad derivada, formada por la dimensión de longitud elevada al cubo [L]3, por lo cual las unidades de volumen son:
• En el Sistema Internacional de Unidades: metros cúbicos (m3)
• En el en sistema Inglés: pies cúbicos (pies3)
• En el sistema CGS: centímetros cúbicos (cm3)
En general, cualquier longitud al cubo sirve para expresar un volumen, por ejemplo, pulgadas al cubo (pulg3), yardas cúbicas (yd3), milímetros cúbicos (mm3), kilómetros cúbicos (km3), etc.; ya sea que se trate de una sustancia sólida, líquida o gaseosa.
En cuanto a las propiedades físicas de las sustancias, estas pueden ser intensivas o extensivas, y en lo que respecta al volumen, se trata de una cantidad extensiva, es decir, su valor depende de la cantidad de materia.
Por otra parte, desde el punto de vista práctico, el volumen se considera una medida indirecta, ya que su valor se determina a partir de ecuaciones que involucran dos o más medidas directas, las cuales son determinadas con instrumentos para medir longitud, por ejemplo, para calcular el volumen de un cilindro de base circular, no se dispone de un instrumento que directamente sirva para medir este volumen, en cambio, se mide su altura y diámetro y estos valores se sustituyen en la fórmula para el cálculo del volumen de un cilindro.
Volumen de figuras geométricas
Toda materia ocupa un volumen en el espacio, sin embargo, no se dispone de fórmulas para calcular los infinitos volúmenes que existen. Para cuerpos geométricos comunes, se dispone de fórmulas que permiten determinar fácilmente este parámetro en dichas figuras. Por ejemplo, para figuras de sección transversal constante, digamos los cubos, paralelepípedos, cilindros, o prismas de sección regular; el volumen se halla multiplicando el área de su base por la altura.
La siguiente tabla muestra algunas fórmulas de volúmenes para figuras geométricas comunes:
Cubo
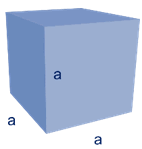
\(V={{a}^{3}}\)
Paralelepípedo
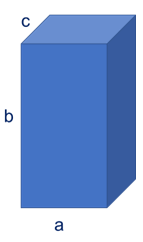
\(V= a \cdot b \cdot c\)
Cilindro de base circular
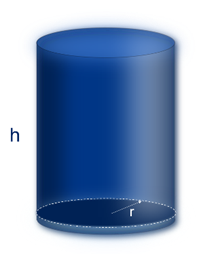
\(V=\pi \cdot {{r}^{2}} \cdot h\)
Esfera
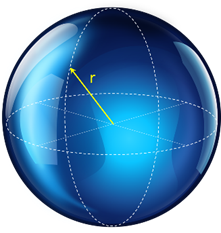
\(V=\frac{4}{3} \cdot \pi \cdot {{r}^{3}}\)
Pirámide de base cuadrada
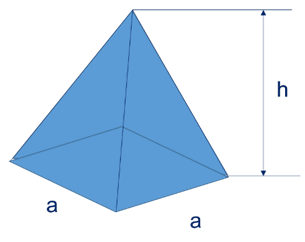
\(V=\frac{1}{3} \cdot {{a}^{2}} \cdot h\)
Cono
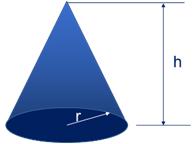
\(V=\frac{1}{3} \cdot \pi \cdot {{r}^{2}} \cdot h\)
• Cuando el cuerpo es un sólido de forma irregular, se emplean otros métodos o técnicas para determinar su volumen, por ejemplo, sumergir el cuerpo en un fluido de densidad conocida (agua) contenido en un recipiente escalado y calibrado, de manera que el volumen del fluido desplazado equivale al volumen del cuerpo.
• Asimismo, en algunas aplicaciones en las cuales se conocen las ecuaciones de las superficies que delimitan el contorno del cuerpo, se pueden utilizar integrales para calcular el volumen del sólido.
• En el caso de figuras compuestas, como un cascarón esférico hueco o una tubería con un determinado espesor de pared, el volumen del sólido se puede calcular a partir de la diferencia del volumen de la figura externa, menos el volumen que ocupa la región hueca.
Relación entre el volumen y la capacidad
La capacidad se refiere al espacio vacío de algún objeto que puede contener un volumen, por lo tanto, existe una relación entre la capacidad y el volumen. Así pues, es posible experimentalmente demostrar que si se dispone de un recipiente calibrado con capacidad de 1 litro y se llena con el agua que estaba contenida en un cubo cuyas aristas miden 10 cm, se puede determinar que 1 litro de agua es equivalente a 1000 cm3 de esta sustancia (10 cm x 10 cm x 10 cm = 1000 cm3).
Ejemplo de cálculo de volumen
Se desea determinar el volumen en m3 de un cilindro cuyas dimensiones se muestran en la imagen:
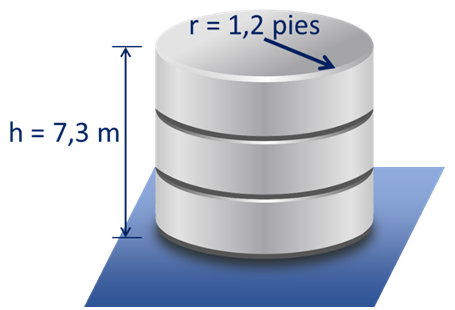
En este caso, el primer paso requiere efectuar una conversión de unidades a fin de unificar las dimensiones. Se sabe que 1 pie = 0,3048 m.
\(1,2~pies\times \frac{0,3048~m}{1~pie}=0,3658~m\)
Teniendo las unidades en el mismo sistema, se procede a determinar el volumen del cilindro:
\(V=\pi \cdot {{r}^{2}} \cdot h=\pi \cdot {{\left( 0,3658 \right)}^{2}} \cdot \left( 7,3 \right)\)
El volumen del cilindro es:
V = 3,07 m3
Aplicaciones del volumen
En Física, Química y otras áreas, no solo es importante conocer el volumen de un cuerpo en sí mismo; además, este valor suele ser de gran utilidad para desarrollar otros cálculos o análisis, por ejemplo, el volumen sirve para:
• Expresar la concentración de una sustancia
• Calcular la densidad de un cuerpo o material
• Determinar la fuerza de flotación que ejerce un líquido
• Hallar la fuerza que le aplica un fluido sobre una superficie sumergida

Art. actualizado: Julio 2022; sobre el original de enero, 2009.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.