Definición de Torsor

Ingeniera Industrial, MSc en Física, y EdD
El torsor se refiere a un sistema fuerza – par en el cual ambos vectores se encuentran en la misma línea de acción. Esto significa que el efecto que le provoca un torsor a un objeto es una traslación más una rotación respecto al mismo eje.
¿Cómo se obtiene una llave de torsión?
En muchos casos, cuando se transforma un sistema general de cargas, a un sistema fuerza par, es posible que este último no sea perpendicular. En esta situación, no es posible reducirlo hasta una sola fuerza resultante equivalente en otro punto.
Por lo general, cuando el sistema de fuerzas no son paralelas, ni coplanares, ni concurrentes, el sistema fuerza – par que generan no es perpendicular; sin embargo, esto no es una regla. Cuando no resulte evidente si el sistema fuerza – par es perpendicular, es necesario comprobar esta condición para determinar su posible reducción.
La forma de obtener una llave de torsión inicia a partir de un sistema de fuerzas y/o pares (momentos o torcas) que están aplicados a un cuerpo rígido en diferentes puntos. Para reducir el sistema, el primer paso consiste en mover todas las fuerzas a un punto arbitrario para convertirlas en fuerzas concurrentes y poderlas sumar y obtener la llamada fuerza resultante (\(\vec R\)).
Ahora bien, cuando se mueven fuerzas de un punto a otro, fuerza de su línea de acción, se deben agregar pares (momentos) perpendiculares a dicha fuerza. De esta manera, al calcular la fuerza resultante, también habrá que determinar un momento resultante (\({\vec M_R}\)), que no es más que la suma de todos los pares que originaron las fuerzas al moverlas.

Si al sistema fuerza – par obtenido, se le determina el producto escalar y el resultado es diferente de cero, se demuestra que dicho sistema no es perpendicular (θ ≠ 90°), y es entonces cuando se puede obtener la llave de torsión o torsor.
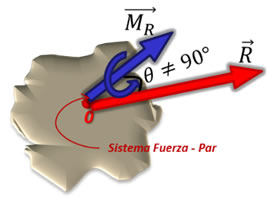
Si se continúa desarrollando un sistema fuerza – par no perpendicular para reducirlo, el siguiente paso es descomponer el momento resultante con respecto a la fuerza resultante, de modo que una componente quedará paralela (MII) a la fuerza y la otra componente perpendicular (M⊥) a dicha fuerza. Se sustituye entonces el momento resultante por sus componentes (vectores en color verde mostrados en la siguiente imagen).
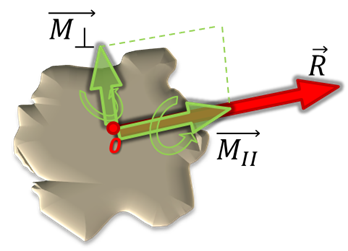
El momento paralelo (MII), representa la proyección del momento resultante (MR) sobre la fuerza resultante (R), la cual se determina mediante el siguiente producto escalar:
\({M_{II}} = \overrightarrow {{M_R}} \cdot \widehat {_R}\)
Donde \(\widehat {_R}\) es el vector unitario de la fuerza resultante, es decir.
\(\widehat {_R} = \frac{{\vec R}}{R}\)
Ya que el producto escalar da como resultado un escalar, la expresión anterior representa el valor escalar del momento paralelo. Este escalar permite comprobar si el sistema fuerza –par obtenido es perpendicular o no, en otras palabras:
Si (MII) = 0 → θ = 90° y el sistema se puede reducir a una resultante (R) equivalente en otro punto.
Si (MII) ≠ 0 → θ ≠ 90° y el sistema se puede reducir a una llave de torsión equivalente en otro punto.
No obstante, el momento paralelo es una cantidad vectorial, así, si su escalar resulta diferente de cero, implica que el sistema se reducirá hasta un torsor equivalente y será necesario determinar el momento paralelo en forma vectorial como sigue:
\(\overrightarrow {{M_{II}}} = {M_{II}} \cdot \widehat {_R}\)
Si la reducción del sistema corresponde a una llave de torsión equivalente en otro punto, es necesario determinar el respectivo Paso (P) de dicho torsor.
\(P = \frac{{{M_{II}}}}{R}\)
Como se observa, el paso es una cantidad escalar, y expresa el desplazamiento recorrido por la llave de torsión en cada vuelta. Debido a que el paso representa el escalar de un desplazamiento, sus unidades deben ser las de longitud (metro, milímetros, pulgadas, pies, entre otras).
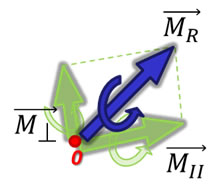
Una vez conocido el momento resultante y el momento paralelo, se determina por diferencia (de la ley del paralelogramo) la componente del momento perpendicular (M⊥) como sigue:
\(\overrightarrow {{M_R}} = \overrightarrow {{M_{II}}} + \overrightarrow {{M_{⊥}}} \)
despejando queda:
\(\overrightarrow {{M_{}}} = \overrightarrow {{M_R}} + \overrightarrow {{M_{II}}} \)
Por otra parte, la componente perpendicular del momento y la fuerza resultante conforman un sistema fuerza – par perpendicular, en consecuencia, se puede reducir a una resultante equivalente en otro punto, digamos A (determinado a partir del vector posición de la fuerza resultante).
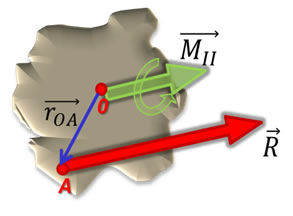
Del mismo modo, que para un sistema fuerza – par perpendicular, el vector posición de la fuerza resultante se determinará a partir de la expresión:
\(\overrightarrow {{M_{}}} = \overrightarrow {{r_{0A}}} \times \vec R\)
Finalmente, dado que el momento es un vector libre (se puede ubicar en cualquier parte), moveremos este vector hasta el punto de aplicación de la fuerza resultante, formando así, un sistema fuerza par que tiene la misma línea de acción, como se indica en la figura.
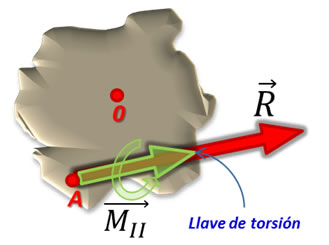
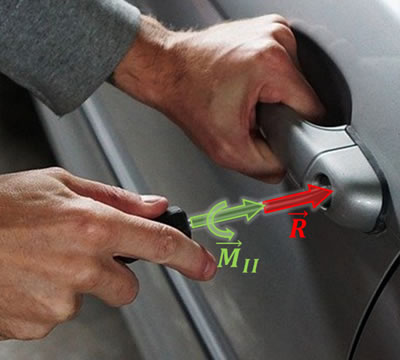
A este sistema se le conoce como llave de torsión o torsor y se puede relacionar con el efecto que le produce un destornillador a un cuerpo rígido, en el sentido que a través de esta herramienta, se aplica una fuerza y al mismo tiempo, se ejerce una rotación (par) alrededor de la misma línea de acción.
Haciendo la analogía de un torsor con el efecto producido con un destornillador, se tiene que un paso positivo (P > 0), implica que tanto la fuerza resultante como el momento paralelo se encuentran en el mismo sentido. Por el contrario, si el paso resulta ser negativo (P < 0), la fuerza resultante y el momento paralelo estarán en sentido contrario.

Trabajo publicado en: Sep., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.