Definición de Teorema de Pitágoras

Maestría en Matemáticas, Dr. en Ciencias
El Teorema de Pitágoras determina que, en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. En el triángulo \(ABC\) con ángulo recto en el vértice \(C\) se tiene:
\({a^2} + {b^2} = {c^2}\)
El Teorema de Pitágoras es uno de los más conocidos y se tienen registros que muestra que ya era usado en diferentes culturas antiguas a lo largo de la historia de la humanidad. Ha contribuido en el desarrollo de varias áreas de la Matemática como la Trigonometría, Geometría Analítica, Cálculo, etc.
Triángulos Rectángulos. Propiedades Básicas.
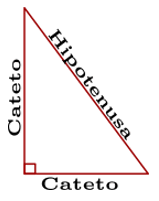
Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, que mida 90° ( \(\frac{\pi }{2}\) radianes); los catetos constituyen los lados del ángulo recto, por su parte la hipotenusa comprende el lado en oposición al ángulo recto.
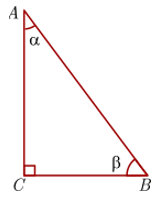
Los ángulos no rectos de un triángulo rectángulo son ángulos complementarios, es decir si los ángulos no rectos miden \(\alpha \) y \(\beta \) entonces:
\(\alpha + \beta = 90^\circ \)
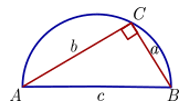
El triángulo rectángulo está inscrito en una circunferencia cuyo centro está en el punto medio de la hipotenusa y esta es un diámetro de dicha circunferencia.
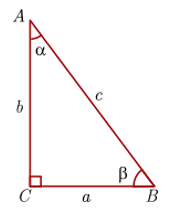
Teorema de Pitágoras
El Teorema de Pitágoras afirma lo siguiente:
En un triángulo rectángulo, la suma de los cuadrados de los catetos resulta igual al cuadrado de la hipotenusa. En el triángulo \(ABC\) con ángulo recto en el vértice \(C\) se tiene:
\({a^2} + {b^2} = {c^2}\)
Al situar un cuadrado sobre cada cateto, y en el mismo orden, uno sobre la hipotenusa, la suma de las áreas de ambos cuadrados sobre los catetos es igual al área del cuadrado situado sobre la hipotenusa; es decir:
\({A_1} + {A_2} = {A_3}\)
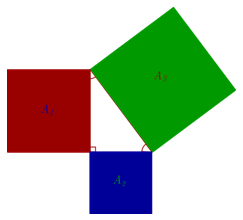
Lo mismo sucede si montamos sobre los catetos una semicircunferencia o un triángulo equilátero en cada uno de los catetos y otra semicircunferencia o triángulo equilátero sobre la hipotenusa
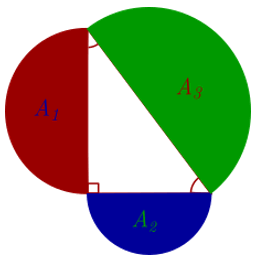
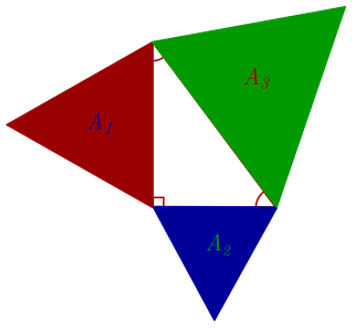
En las imágenes anteriores se cumple:\({A_1} + {A_2} = {A_3}\)
Ejemplos de aplicación del Teorema de Pitágoras
Aplicación 1
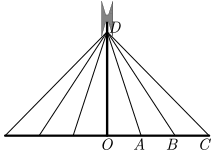
Una antena, a una altura de 10 m, será sujetado con cables como se muestra en la figura, en donde \(OA = 3{\rm{m}},\;OB = 6{\rm{m}}\;{\rm{y}}\;OC = 9{\rm{m}}\). Calcule la longitud de cada uno de los cables que serán usados.
Planteamiento: La antena está colocada de manera perpendicular por lo cual el triángulo donde el ángulo recto tiene vértice por lo tanto los segmentos \(\overline {DO} \) y \(\overline {OA} \) son catetos y \(\overline {DA} \) es hipotenusa. Algo similar sucede con los demás triángulos.
Solución
| Cateto 1 | Cateto 2 | Hipotenusa |
|---|---|---|
| 10 | 3 | \(\sqrt {{{10}^2} + {3^2}} = \sqrt {109} \) |
| 10 | 6 | \(\sqrt {{{10}^2} + {3^2}} = \sqrt {136} = 2\sqrt {34} \) |
| 10 | 9 | \(\sqrt {{{10}^2} + {9^2}} = \sqrt {181} \) |
Respuesta: Se necesitarán 2 cables que midan \(\sqrt {109} {\rm{m}} \approx 10.44{\rm{m}}\), dos de \(2\sqrt {34} {\rm{m}} \approx 11.662{\rm{m}}\) y dos de \(\sqrt {181} {\rm{m}} \approx 13.454{\rm{m}}\)
Aplicación 2

Es usual que cuando anuncian el tamaño de un televisor sólo mencionan una medida y ésta corresponde a la diagonal del televisor; por ejemplo, cuando dicen que es un televisor es de 22 in; lo que nos están diciendo es que la diagonal del televisor mide 22 in. En algunos casos mencionan el formato de la televisión y los formatos más usuales son 4:3 y 16:9. En el primer caso nos están diciendo: \(\frac{{{\rm{base}}}}{{{\rm{altura}}}} = \frac{4}{3}\) para el primer caso y para el segundo \(\frac{{{\rm{base}}}}{{{\rm{altura}}}} = \frac{{16}}{9}\).
En caso de conocer la longitud de la diagonal \(d\), de un televisor; determinar cuánto miden su base y su altura, cuando el televisor tiene un formato 4:3.
En caso de conocer la longitud de la diagonal de un televisor; determinar cuánto miden su base y su altura, cuando el televisor tiene un formato 4:3.
Planteamiento del problema
Caso formato 4:3.
Denotaremos con \(b\) la longitud de la base, con \(a\) la longitud de la altura y con \(d\) la longitud de la diagonal.
Se tiene lo siguiente:
\(\frac{b}{a} = \frac{4}{3}\)
De manera equivalente:
\(b = \frac{4}{3}a\)
Aplicando el Teorema de Pitágoras tendremos:
\({a^2} + {b^2} = {d^2}\)\({a^2} + {\left( {\frac{4}{3}a} \right)^2} = {d^2}\)
Caso formato 16:9.
De manera análoga al caso formato 4:3, se establece la ecuación:
\({a^2} + {\left( {\frac{{16}}{9}a} \right)^2} = {d^2}\)
Solución
Formato 16:9
| \({a^2} + {\left( {\frac{4}{3}a} \right)^2} = {d^2}\) | Situación inicial |
|---|---|
| \({a^2} + \frac{{16}}{9}{a^2} = {d^2}\) | Se elevó al cuadrado. |
| \(9{a^2} + 16{a^2} = 9{d^2}\) | Se multiplicó por 9, cada lado de la ecuación. |
| \(25{a^2} = 9{d^2}\) | Se simplificó. |
| \(\sqrt {25{a^2}} = \sqrt {9{d^2}} \) | Se sacó raíz cuadrada de cada lado. |
| \(5\left| a \right| = 3\left| d \right|\) | Hay que considerar que, por ser longitudes, las variables involucradas deben ser mayores o iguales que cero. |
| \(a = \frac{3}{5}d\) | Se dividió entre 5 cada lado de la ecuación. |
Como:
\(b = \frac{4}{3}a\)\(\;\;\;\; = \frac{4}{3}\left( {\frac{3}{5}d} \right)\)\(\;\;\;\; = \frac{4}{5}d\)
Formato 16:9
| \({a^2} + {\left( {\frac{{16}}{9}a} \right)^2} = {d^2}\) | Situación inicial |
|---|---|
| \({a^2} + \frac{{256}}{{81}}{a^2} = {d^2}\) | Se elevó al cuadrado. |
| \(81{a^2} + 256{a^2} = 81{d^2}\) | Se multiplicó por 81, cada lado de la ecuación. |
| \(337{a^2} = 81{d^2}\) | Se simplificó |
| \(\sqrt {337{a^2}} = \sqrt {81{d^2}} \) | Se sacó raíz cuadrada de cada lado. |
| \(\sqrt {337} \left| a \right| = 9\left| d \right|\) | Hay que considerar que, por ser longitudes, las variables involucradas deben ser mayores o iguales que cero. |
| \(a = \frac{9}{{\sqrt {337} }}d\) | Se dividió entre 5 cada lado de la ecuación. |
| \(a = \frac{{9\sqrt {337} }}{{337}}d\) | Se multiplicó el denominador y numerador por \(\sqrt {337} \) |
Como:
\(b = \frac{{16}}{9}a\)\(\;\;\;\; = \frac{{16}}{9}\left( {\frac{{9\sqrt {337} }}{{337}}d} \right)\)\(\;\;\;\; = \frac{{16\sqrt {337} }}{{337}}d\)
Respuesta:
En el formato 4:3 se cumplen las siguientes relaciones:
\(a = \frac{3}{5}d\)\(b = \frac{4}{5}d\)
En el formato 16:9 se cumplen las siguientes relaciones:
\(a = \frac{{9\sqrt {337} }}{{337}}d\)\(b = \frac{{16\sqrt {337} }}{{337}}d\)
Aplicación 3
Se desea construir una caja de 60cm de largo, como la que se muestra en el siguiente esquema:
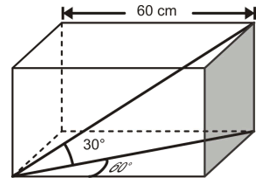
Hallar el ancho y el alto de la caja.
Planteamiento del Problema
Consideremos los siguientes dos esquemas
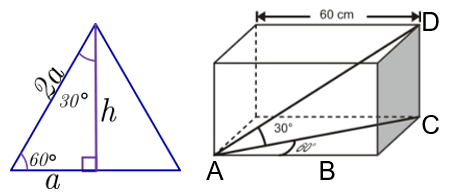
En el triángulo rectángulo 30°-60°, si el lado opuesto al ángulo de 30° mide \(a\), entonces la hipotenusa mide \(2a\). En nuestro caso \(AB = 60\) de donde concluimos que \(AC = 120.\)
En el caso del triángulo \(ACD\) el lado \(AC\) es el cateto adyacente al de 30° entonces debe cumplirse:\(AC = \sqrt 3 CD.\;\)
Solución
\({\left( {AB} \right)^2} + \left( {BC} \right)_{}^2 = {\left( {AC} \right)^2}\)
\({\left( {60} \right)^2} + {\left( {BC} \right)^2} = {120^2}\)
\({\left( {BC} \right)^2} = {120^2} – {60^2} = 10800\)
\(BC = 60\sqrt 3 \)
Como
\(\;\;\;\;\;\;\;AC = \sqrt 3 CD\)
\(\;\;\;\;\;120 = \sqrt 3 CD\)
\(\;\;\;\;\;\frac{{120}}{{\sqrt 3 }} = CD\)
\(\frac{{120\sqrt 3 }}{3} = CD\)
\(\;\;40\sqrt 3 = CD\)
Respuesta
El ancho de la es de \(60\sqrt 3 \;\)cm mientras que el alto mide \(40\sqrt 3 \)cm.
Aplicación 4
Planteamiento del problema: Las diagonales de un rombo miden 30 cm y 16 cm, hallar la medida del lado del rombo. Las diagonales de un rombo se cortan en su punto medio y son perpendiculares; por lo cual se tiene un triángulo rectángulo cuyos catetos miden 15 cm y 8 cm y la longitud de la hipotenusa es igual a la longitud del lado del rombo
Solución
\(\;{15^2} + {8^2} = {c^2}\)\(225 + 65 = {c^2}\)\(\;\;\;\;\;\;\;\;\;\;289 = {c^2}\)\(\;\;\;\;\;\;\;\sqrt {289} = \sqrt {{c^2}} \)\(\;\;\;\;\;\;\;\;\;\;\;\;17 = \left| c \right|\)
Respuesta: El lado del rombo mide 17 cm
Aplicación 5
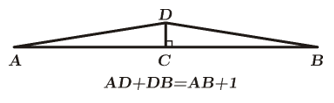
En los puntos \(A\) y \(B\) se fija un alambre de longitud \(AB + 1;\) sea \(C\) el punto medio del segmento \(\overline {AB} \), y \(D\) el punto medio del alambre. Desde el punto \(C\) se tensa el alambre, por su punto medio \(D\), formando un triángulo isósceles, como se muestra en el esquema. Si \(AB = 10m,\) ¿Por el punto C puede pasar caminando un gato, sin que le estorbe el alambre?
Planteamiento del problema
Una estimación sin cálculo se puede llegar a pensar que el segmento \(DC\) es muy pequeño.
Por las condiciones del problema se tiene que el triángulo \(ADC\)es rectángulo cuya hipotenusa mide 5.5 m y uno de sus catetos mide 5m.
Solución
\({\left( {AC} \right)^2} + {\left( {DC} \right)^2} = {\left( {AD} \right)^2}\)
\(\;\;\;\;\;\;\;{5^2} + {\left( {DC} \right)^2} = {5.5^2}\)
\(\;\;\;\;\;\;\;25 + {\left( {DC} \right)^2} = 30.25\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {DC} \right)^2} = 5.25\)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sqrt {{{\left( {DC} \right)}^2}} = \sqrt {5.25} \)
\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {DC} \right| \approx 2.2913\)
Respuesta: El valor de \(DC \approx 2.2913\). por lo cual un gato puede pasar en medio del triángulo formado sin ningún problema.
Ejemplos prácticos
El Teorema de Pitágoras permite saber la longitud de la hipotenusa si se conoce la longitud de los catetos.
| Longitud de un cateto (\(a\)) | Longitud del otro cateto (\(b\)) | Longitud de la hipotenusa (\(c\)) |
|---|---|---|
| 1 | 1 | \(\sqrt {{1^2} + {1^2}} = \sqrt 2 \) |
| 1 | 2 | \(\sqrt {{1^2} + {2^2}} = \sqrt 5 \) |
| 8 | 15 | \(\sqrt {{8^2} + {{15}^2}} = \sqrt {289} = 17\) |
| 7 | 5 | \(\sqrt {{7^2} + {5^2}} = \sqrt {74} \) |
| 40 | 9 | \(\sqrt {{{40}^2} + {{41}^2}} = \sqrt {1681} = 41\) |
En caso de que se conozca la longitud de la hipotenusa y de uno de los catetos, se puede saber la longitud del otro cateto al establecer la ecuación:
\({a^2} + {x^2} = {c^2}\)\({x^2} = {c^2} – {a^2}\)\(x = \sqrt {{c^2} – {a^2}} \)
| Longitud de un cateto (\(a\)) | Longitud de la hipotenusa (\(c\)) | Longitud del otro cateto (b) |
|---|---|---|
| 1 | 2 | \(\sqrt {{2^2} – {1^2}} = \sqrt 3 \) |
| 8 | 15 | \(\sqrt {{{15}^2} – {8^2}} = \sqrt {161} \) |
| 65 | 16 | \(\sqrt {{{65}^2} – {{16}^2}} = \sqrt {3969} = 63\) |
| 28 | 53 | \(\sqrt {{{53}^2} – {{28}^2}} = \sqrt {2025} = 45\) |
| 29 | 20 | \(\sqrt {{{29}^2} – {{20}^2}} = \sqrt {441} = 21\) |
Recíproco del Teorema de Pitágoras
Se tienen registros que los agrimensores del antiguo Egipto usaban una cuerda con doce nudos igualmente espaciados y con ella formar un triángulo cuyos lados medían: 3,4,5 “nudos”, de este modo obtenían un triángulo rectángulo, sin saberlo, estaban usando el teorema llamado el recíproco del Teorema de Pitágoras, el cual dice:
Dado un triángulo cuyos lados miden \(a,b\) y \(c\), si se cumple la siguiente relación:
\({a^2} + {b^2} = {c^2}\)
Entonces el triángulo es rectángulo cuyo ángulo recto es opuesto al lado mide \(c\), o de manera equivalente, el ángulo recto está formado por los lados cuyas longitudes son \(a\) y \(b.\)
Como \({3^2} + {4^2} = {5^2}\) entonces se cumplen las condiciones del recíproco del Teorema de Pitágoras y estamos ante un triángulo rectángulo.
Lo anterior justifica que el método usado por los agrimensores del antiguo Egipto era correcto para formar un ángulo de 90°.
Ejemplos Prácticos
Para deducir si un triángulo es rectángulo, de preferencia, hay que ordenar de menor a mayor las medidas de sus lados; sumar los cuadrados de los dos lados menores y compararlo con el cuadrado del lado mayor.
| Lado 1 | Lado 2 | Lado 3 | \({a^2} + {b^2}\) | \({c^2}\) | Triángulo rectángulo |
|---|---|---|---|---|---|
| 5 | 12 | 13 | \({5^2} + {12^2} = 169\) | \({13^2} = 169\) | Sí |
| 5 | 10 | 14 | \({5^2} + {10^2} = 125\) | \({14^2} = 196\) | No |
| 7 | 24 | 25 | \({7^2} + {24^2} = 625\) | \({25^2} = 225\) | Sí |
| 8 | 10 | 11 | \({8^2} + {10^2} = 164\) | \({11^2} = 121\) | No |
| 8 | 10 | 2\(\sqrt {41} \) | \({8^2} + {10^2} = 164\) | \({\left( {2\sqrt {41} } \right)^2} = 4\left( {41} \right) = 164\) | Sí |
Triángulos especiales
Las escuadras escolares y profesionales suelen ser de diferentes tamaños, pero los ángulos siempre miden lo mismo -45°-45°-90° y la otra es de 30°-60°-90°.
Triángulo Rectángulo 45°-45°
De un cuadrado de lado \(a\), al trazar una de sus diagonales se obtienen dos triángulos rectángulos isósceles, mediante el teorema de Pitágoras encontraremos una relación entre la longitud del lado del cuadrado y la longitud de su diagonal.
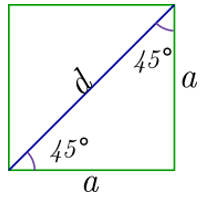
Por el Teorema de Pitágoras:
\({a^2} + {a^2} = {d^2}\)\(2{a^2} = {d^2}\)\(\sqrt 2 a = d\)
Triángulo Rectángulo 30°-60°
De un triángulo equilátero de lado \(2a\), al trazar una de sus alturas se obtienen dos triángulos rectángulos que tienen las mismas medidas, mediante el teorema de Pitágoras encontraremos una relación entre la longitud del lado del triángulo equilátero de lado \(2a\) y la longitud de su altura.
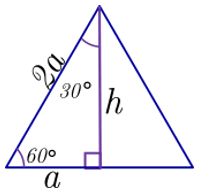
Por el Teorema de Pitágoras:
\({a^2} + {h^2} = {\left( {2a} \right)^2}\)\({a^2} + {h^2} = 4{a^2}\)\({h^2} = 3{a^2}\)\(h = \sqrt 3 a\)
Siga en Teorema de Pitágoras (parte 2)

Art. actualizado: Dic. 2022; sobre el original de noviembre, 2011.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.