Definición de Números Complejos

Maestría en Matemáticas, Dr. en Ciencias
Debido a que para cualquier \(x \in \mathbb{R}\), se cumple \(x\)2\( \ge 0\) entonces para \(s < 0\) las ecuaciones de la forma:
\({x^2} = s\)
No tiene solución en los números reales.
Los números complejos son una extensión de los números reales, donde hay raíces cuadradas de números negativos, de hecho, se puede definir la unidad imaginaria \(i\) como \(i = \sqrt { - 1} \), es decir:
\({i^2} = - 1.\)
A partir de la definición, tendremos que:
\({\left( {5i} \right)^2} = {5^2}{i^2} = 25\left( { – 1} \right) = – 25\)
\({\left( { – 5i} \right)^2} = {\left( { – 5} \right)^2}{i^2} = 25\left( { – 1} \right) = – 25\)
Por lo cual la ecuación \({x^2} + 25 = 0\), ya tiene dos soluciones, a saber: \(\alpha = 5i\) y \(\beta = – 5i\)
Al aplicar la fórmula general para resolver la ecuación: \({x^2} – 6x + 25\); se obtiene que el discriminante: \({b^2} – 4ac = {( – 6)^2} – 4\left( 1 \right)\left( {25} \right) = 36 – 100 = – 64 < 0\). De donde se concluye que esta ecuación no tiene solución en los números reales, pero \({(8i)^2} = – 64\) y al aplicar la fórmula general, se obtiene:
\(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}} = \frac{{6 \pm \sqrt { – 64} }}{2} = \frac{{6 \pm 8i}}{2} = 3 \pm 4i\)
Lo anterior sugiere que tenemos dos soluciones de la ecuación, \({x^2} – 6x + 25 = 0\).
Un número complejo \(z\), se define como:
\(z = a + ib\)
Donde \(a,b \in \mathbb{R}\). El número a es llamado la parte real de \(z\) mientras que \(b\) es llamada su parte imaginaria de manera simbólica:
\({\rm{Re}}\left( z \right) = a,\;\;{\rm{Im}}\left( z \right) = b\)
Denotaremos con \(\mathbb{C}\) al conjunto de los números complejos, es decir:
\(\mathbb{C} = \left\{ {a + ib\;|\;a,b \in \mathbb{R}} \right\}\)
Un número real se puede considerar como un número complejo cuya parte imaginaria, es decir:
\(x = x + 0i\)
Un número de la forma \(ib\) es llamado imaginario puro.
Operaciones Básicas de Números Complejos
A continuación, \(z = a + ib\), \(w = c + id\).
Suma y resta de números complejos
\(z + w = \left( {a + c} \right) + \left( {b + d} \right)i\)
\(z – w = \left( {a – c} \right) + \left( {b – d} \right)i\)
Ejemplos
\(\left( {5 – 3i} \right) + \left( { – 7 + 4i} \right) = \left( {5 – 7} \right) + \left( { – 3 + 4} \right)i = – 2 + i\)
\(\left( {5 – 3i} \right) – \left( { – 7 + 4i} \right) = \left( {5 – \left( { – 7} \right)} \right) + \left( { – 3 – \left( 4 \right)} \right)i = 12 – 7i\)
Producto de números complejos
Para realizar el producto de números complejos se realiza un proceso similar a cuando se multiplican dos binomios
\(zw = \left( {a + ib} \right)\left( {c + di} \right)\)
\(\; = \left( {a + ib} \right)c + \left( {a + ib} \right)di\)
\(\; = ac + bci + adi + bd{(i)^2}\)
\(\; = ac – bd + \left( {ad + bc} \right)i\)
Ejemplos
\(\left( {5 – 3i} \right)\left( { – 7 + 4i} \right) = \left( {5 – 3i} \right)\left( { – 7} \right) + \left( {5 – 3i} \right)\left( {4i} \right)\)
\(\; = 5\left( { – 7} \right) + \left( { – 3i} \right)\left( { – 7} \right) + 5\left( {4i} \right) + \left( { – 3i} \right)\left( {4i} \right)\)
\(\; = – 35 + 21i + 20i – 12{i^2}\)
\(\; = – 35 – 12\left( { – 1} \right) + \left( {21 + 20} \right)i\)
\(\; = – 23 + 41i\)
\(\left( {5 + 3i} \right)\left( {7 + 4i} \right) = \left( {5 + 3i} \right)7 + \left( {5 + 3i} \right)4i\)
\(\; = 5\left( 7 \right) + \left( 3 \right)7i + 5\left( {4i} \right) + 3\left( 4 \right){i^2}\)
\(\; = 35 + \left( {21 + 20} \right)i – 12\)
\(\; = 23 + 41i\)
El conjugado de un número complejo
Dado un número complejo \(z = a + ib,\;\)se define el conjugado de \(z\;\)como:
\(\bar z = \overline {a + bi} = a – bi\)
Además, se cumple:
\(\;\;\;\;\;\;\;\;\;\;\;z\bar z = \left( {a + bi} \right)\left( {a – bi} \right)\)
\( = {a^2} + {b^2}\)
Ejemplos
\(\overline { – 3 + 4i} = – 3 – 4i\)\(\overline {\;\;\;3 – 4i} = 3 – \left( { – 4} \right)i = 3 + 4i\)\(\left( { – 5 – 12i} \right)\overline {\left( { – 5 – 12i} \right)} = \left( { – 5 – 12i} \right)\left( { – 5 + 12i} \right) = {5^2} + {12^2} = 169\)
División con números complejos
Cuando hacemos la división \(\frac{x}{y},\;y \ne 0,\) es equivalente a realizar el producto \(x{y^{ – 1}},\;\) donde \({y^{ – 1}}\) es el inverso multiplicativo
Cuando hacemos la división \(\frac{x}{y},\;y \ne 0,\) es equivalente a realizar el producto \(x{y^{ – 1}},\;\) donde \({y^{ – 1}}\) es el inverso multiplicativo de \(y\), esto es: \(y{y^{ – 1}} = 1\).
Inverso multiplicativo de un número complejo
Para un número complejo \(z = a + ib\), distinto de cero, se tiene que:
\({z^{ – 1}} = \frac{{\bar z}}{{{a^2} + {b^2}}} = \frac{{a – ib}}{{{a^2} + {b^2}}} = \frac{a}{{{a^2} + {b^2}}} + \frac{b}{{{a^2} + {b^2}}}i,\)
En efecto:
\(z\left( {\frac{{\bar z}}{{{a^2} + {b^2}}}} \right) = \frac{{z\bar z}}{{{a^2} + {b^2}}} = \frac{{{a^2} + {b^2}}}{{{a^2} + {b^2}}} = 1\)
Ejemplos
\({\left( {5 – 12i} \right)^{ – 1}} = \frac{{\overline {5 – 12i} }}{{{5^2} + {{12}^2}}} = \frac{{5 – \left( { – 12} \right)i}}{{169}} = \frac{{5 + 12i}}{{169}} = \frac{5}{{169}} + \frac{{12}}{{169}}i\)
\({\left( { – 3 + 4i} \right)^{ – 1}} = \frac{{\overline { – 3 + 4i} }}{{{3^2} + {4^2}}} = \frac{{ – 3 – \left( 4 \right)i}}{{25}} = \frac{{ – 3 – 4i}}{{25}} = – \frac{3}{{25}} – \frac{4}{{25}}i\)
División de números complejos
Para \(w \ne 0\) se define
\(\frac{z}{w} = z{w^{ – 1}} = z\frac{{\bar w}}{{w\bar w}} = \frac{{z\bar w}}{{w\bar w}}\)
De manera práctica, para realizar la división entre dos números complejos, lo que se realiza es multiplicar el dividendo y el divisor por el conjugado del divisor.
Ejemplos
\(\frac{{5 – 12i}}{{3 – 4i}} = \frac{{\left( {5 – 12i} \right)\left( {\overline {3 – 4i} } \right)}}{{\left( {3 – 4i} \right)\left( {\overline {3 – 4i} } \right)}} = \frac{{\left( {5 – 12i} \right)\left( {3 + 4i} \right)}}{{\left( {3 – 4i} \right)\left( {3 + 4i} \right)}} = \frac{{5\left( 3 \right) – 12\left( 4 \right){i^2} + \left( {5\left( 4 \right) + \left( { – 12} \right)3} \right)i}}{{{3^2} + {4^2}}}\)\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{15 + 48 + \left( {20 – 36} \right)i}}{{25}} = \frac{{63 – 16i}}{{25}} = \frac{{63}}{{25}} – \frac{{16}}{{25}}i\)
\(\frac{{3 – 4i}}{{5 – 12i}} = \frac{{\left( {3 – 4i} \right)\left( {\overline {5 – 12i} } \right)}}{{\left( {5 – 12i} \right)\left( {\overline {5 – 12i} } \right)}} = \frac{{\left( {3 – 4i} \right)\left( {5 + 12i} \right)}}{{\left( {5 – 12i} \right)\left( {5 + 12i} \right)}} = \frac{{5\left( 3 \right) – 4\left( {12} \right){i^2} + \left( {3\left( {12} \right) + \left( { – 4} \right)5} \right)i}}{{{5^2} + {{12}^2}}}\)\(\; = \frac{{15 + 48 + \left( {36 – 20} \right)i}}{{169}} = \frac{{63 + 16i}}{{169}} = \frac{{63}}{{169}} + \frac{{16}}{{169}}i\)
Representación Geométrica de los Números Complejos
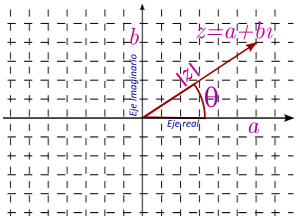
Cada número complejo \(z = a + bi\) puede ser identificado como un vector cuyas coordenadas son \(\left( {a,b} \right)\). Bajo esta óptica el eje \(x\) es llamado eje real y el eje \(y\) es llamado eje imaginario.
Cuando el plano cartesiano es usado para representar números complejos es llamado plano complejo.
La longitud del vector es igual a \(\sqrt {{a^2} + {b^2}} = \sqrt {z\bar z} \) y también tiene asociado un ángulo \(\theta .\)
El módulo de un número complejo \(z = a + ib\) se define como:
\(\left| z \right| = \sqrt {z\bar z} = \sqrt {{a^2} + {b^2}} \)
Si \(a \ne 0\) se define el argumento de un número complejo \(z\) como el ángulo \(\theta \), tal que:
\(\tan \theta = \frac{b}{a},\;\;0 \le \theta < 2\pi \)
Si \(a = 0\) y \(b > 0\), se tiene:
\(\arg \left( z \right) = \frac{\pi }{2}.\)
Si \(a = 0\) y \(b < 0\), se tiene:
\(\arg \left( z \right) = \frac{{3\pi }}{2}\)
Suele denotarse \(\arg \left( z \right) = \theta \).
También se tienen las siguientes relaciones:
\({\rm{cos\;\theta }} = \frac{a}{{\left| z \right|}},\;\;{\rm{\;sin}}\theta = \frac{b}{{\left| z \right|}}\)
El argumento de un número complejo puede calcularse con las funciones inversas de las funciones seno, coseno o tangente, además se debe de tomar en cuenta en que cuadrante del plano está ubicado el número complejo.
Ejemplos
| Nro. Complejo | Módulo nro. complejo | Cálculo con función inversa | Argumento del nro. complejo | |
|---|---|---|---|---|
| \(z = 2\) | \(2\) | \({\rm{arctan}}\frac{0}{2} = 0\) | 0 |
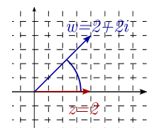 |
| \(w = 2 + 2i\) | \(2\sqrt 2 \) | \({\rm{arctan}}\frac{2}{2} = \frac{\pi }{4}\) | \(\frac{\pi }{4}\) | |
| \(z = 2i\) | \(2\) | \({\rm{arccos}}\frac{0}{2} = \frac{\pi }{2}\) | \(\frac{\pi }{2}\) |
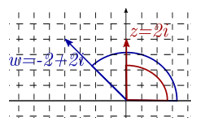 |
| \(w = – 2 + 2i\) | \(2\sqrt 2 \) | \({\rm{arctan}}\frac{{ – 2}}{2} = – \frac{\pi }{4}\) | \(\pi – \frac{\pi }{4} = \frac{{3\pi }}{4}\) | |
| \(z = – 2\) | \(2\) | \({\rm{arccos}}\frac{0}{2} = 0\) | \(\pi \) |
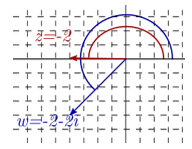 |
| \(w = – 2 + 2i\) | \(2\sqrt 2 \) | \({\rm{arctan}}\frac{{ – 2}}{2} = – \frac{\pi }{4}\) | \(\pi + \frac{\pi }{4} = \frac{{5\pi }}{4}\) | |
| \(z = – 2i\) | \(2\) | \({\rm{arccos}}\frac{0}{2} = \frac{\pi }{2}\) | \(\frac{{3\pi }}{2}\) |
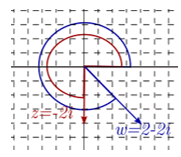 |
| \(w = – 2 – 2i\) | \(2\sqrt 2 \) | \({\rm{arctan}}\frac{{ – 2}}{2} = – \frac{\pi }{4}\) | \(2\pi – \frac{\pi }{4} = \frac{{7\pi }}{4}\) |
Representación polar de un número complejo
Dado un número complejo \(z = a + bi\) cuyo \(\arg \left( z \right) = \theta \); y considerando las relaciones:
\({\rm{cos\;\theta }} = \frac{a}{{\left| z \right|}},\;\;{\rm{\;sin}}\theta = \frac{b}{{\left| z \right|}}\)\(\;\;\;\;\;\;a = \left| z \right|{\rm{cos\;\theta }},{\rm{\;\;}}b = \left| z \right|{\rm{sen\;\theta }}\)
Al utilizar las anteriores relaciones obtenemos:
\(z = a + bi = \;\left| z \right|{\rm{cos\;\theta }} + i\left| z \right|{\rm{sin\;\theta }} = \left| z \right|\left( {{\rm{cos\;\theta }} + i{\rm{sen\;\theta }}} \right)\)
La Fórmula de Euler establece:
\({e^{i\theta }} = {\rm{cos\;\theta }} + i{\rm{sen\;\theta }}\)
Donde \(e\) es la constante de Euler, la base de los logaritmos naturales.
Por lo cual podemos establecer lo siguiente:
\(z = \left| z \right|{e^{i\theta }}\)
Donde \(\theta = \arg \left( z \right).\)
Como \(\cos 0 = \cos 2\pi \) y \(\sin 0 = \sin 2\pi \):
\(1 = {e^{i0}} = {e^{2\pi i}}\)
Como \(\cos \frac{\pi }{2} = 0\) y \(\sin \frac{\pi }{2} = 1\):
\(i = {e^{\frac{\pi }{2}i}}\)
Como \(\cos \frac{{3\pi }}{2} = 0\) y \(\sin \frac{{3\pi }}{2} = – 1\):
\( – i = {e^{\frac{{3\pi }}{2}i}}\)
Como \(\cos \pi = – 1\) y \(\sin \pi = 0:\)
\({e^{\pi i}} = – 1\)
\({e^{\pi i}} + 1 = 0\)
La última relación es llamada la Identidad de Euler y es una de las más fascinantes de la matemática pues relaciona tres de las constantes más importantes de la matemática: \(1,\;e\) y \(\pi .\)
Hemos visto que todo número complejo \(z = a + bi\) se puede expresar como:
\(z = \left| z \right|{e^{i\theta }}\)
La cual es llamada forma polar de un número complejo.
Ejemplos
| Nro. Complejo | Módulo nro. complejo | Argumento del número complejo | Forma polar del nro. complejp |
|---|---|---|---|
| \(2\) | \(2\) | 0 | \(2{e^{i\theta }}\) |
| \(2 + 2i\) | \(2\sqrt 2 \) | \(\frac{\pi }{4}\) | \(2\sqrt 2 {e^{\frac{\pi }{4}i}}\) |
| \(2i\) | \(2\) | \(\frac{\pi }{2}\) | \(2{e^{\frac{\pi }{2}i}}\) |
| \( – 2 + 2i\) | \(2\sqrt 2 \) | \(\frac{{3\pi }}{4}\) | \(2\sqrt 2 {e^{\frac{{3\pi }}{4}i}}\) |
| \( – 2\) | \(2\) | \(\pi \) | \(2{e^{\pi i}}\) |
| \( – 2 + 2i\) | \(2\sqrt 2 \) | \(\frac{{5\pi }}{4}\) | \(2\sqrt 2 {e^{\frac{{5\pi }}{4}i}}\) |
| \( – 2i\) | \(2\) | \(\frac{{3\pi }}{2}\) | \(2{e^{\frac{{3\pi }}{2}i}}\) |
| \( – 2 – 2i\) | \(2\sqrt 2 \) | \(\frac{{7\pi }}{4}\) | \(2\sqrt 2 {e^{\frac{{7\pi }}{4}i}}\) |
Usando la forma polar de un número complejo y a partir de las leyes de los exponentes podemos realizar multiplicaciones, divisiones entre complejas y elevar a una potencia un número complejo.
Supongamos que \(z = \left| z \right|{e^{i\theta }}\) y \(w = \left| w \right|{e^{i\omega }}\), se cumple:
\(zw = \left| z \right|{e^{i\theta }}\left| w \right|{e^{i\omega }} = \left| z \right|\left| w \right|{e^{i\theta }}{e^{i\omega }} = \left| z \right|\left| w \right|{e^{i\left( {\theta + \omega } \right)}}\)\(\frac{z}{w} = \frac{{\left| z \right|{e^{i\theta }}}}{{\left| w \right|{e^{i\omega }}}} = \frac{{\left| z \right|}}{{\left| w \right|}}{e^{i\left( {\theta – \omega } \right)}}{\rm{\;para\;}}w \ne 0\)\({z^k} = {\left( {\left| z \right|{e^{i\theta }}} \right)^k} = {\left| z \right|^k}{e^{ik\theta }}\)
Ejemplos: Producto y división
Para hacer los cálculos hay que tomar en cuenta
\({e^{\pi i}} = – 1,\;\;{e^{\frac{1}{2}\pi i}} = i,\;\;{e^{\frac{3}{2}\pi i}} = – i\;\;\;{e^{2k\pi i}} = 1\;{\rm{para\;}}k \in \mathbb{Z}\)
| \(z\) | \(w\) | \(zw\) | \(\frac{z}{w}\) |
|---|---|---|---|
| \(3{e^{\frac{1}{3}\pi i}}\) | \(2{e^{\frac{1}{4}\pi i}}\) | \(3\left( 2 \right){e^{\frac{1}{3}\pi i}}{e^{\frac{1}{4}\pi i}} = 6{e^{\left( {\frac{1}{3} + \frac{1}{4}} \right)\pi i}}\)= \(6{e^{\left( {\frac{7}{{12}}} \right)\pi i}}\) | \(\frac{{3{e^{\frac{1}{3}\pi i}}}}{{2{e^{\frac{1}{4}\pi i}}}} = \frac{3}{2}{e^{\left( {\frac{1}{3} – \frac{1}{4}} \right)\pi i}} = \frac{3}{2}{e^{\left( {\frac{1}{{12}}} \right)\pi i}}\) |
| \(6{e^{\frac{2}{3}\pi i}}\) | \(2{e^{\frac{1}{6}\pi i}}\) | \(6\left( 2 \right){e^{\frac{2}{3}\pi i}}{e^{\frac{1}{6}\pi i}} = 12{e^{\left( {\frac{2}{3} + \frac{1}{6}} \right)\pi i}}\)= 12\({e^{\left( {\frac{5}{6}} \right)\pi i}}\) | \(\frac{{6{e^{\frac{2}{3}\pi i}}}}{{2{e^{\frac{1}{6}\pi i}}}} = 3{e^{\left( {\frac{2}{3} – \frac{1}{6}} \right)\pi i}} = 3{e^{\left( {\frac{1}{2}} \right)\pi i}} = 3i\) |
| \({e^{\frac{2}{3}\pi i}}\) | \({e^{\frac{7}{4}\pi i}}\) | \({e^{\frac{2}{3}\pi i}}{e^{\frac{7}{4}\pi i}} = {e^{\frac{{29}}{{12}}\pi i}} = {e^{\left( {2 + \frac{5}{4}} \right)\pi i}} = {e^{\frac{{5\pi }}{4}i}}\) | \(\frac{{{e^{\frac{2}{3}\pi i}}}}{{{e^{\frac{7}{4}\pi i}}}} = {e^{ – \frac{{13}}{{12}}\pi i}} = {e^{ – \frac{{13}}{{12}}\pi i}}{e^{2\pi i}} = {e^{\frac{{11}}{{12}}\pi i}}\) |
| \(z\) | \({z^2}\) | \({z^3}\) | \({z^6}\) | \({z^8}\) |
|---|---|---|---|---|
| \(3{e^{\frac{1}{3}\pi i}}\) | \({3^2}{e^{\frac{2}{3}\pi i}}\) | \({3^3}{e^{\frac{3}{3}\pi i}} = 27{e^{\pi i}} = – {3^3}\) | \({3^6}{e^{\frac{6}{3}\pi i}} = {3^6}{e^{2\pi i}} = {3^6}\) | \({3^8}{e^{\frac{8}{3}\pi i}} = {3^8}{e^{2\pi i}}{e^{\frac{2}{3}\pi i}} = {3^8}{e^{\frac{2}{3}\pi i}}\) |
| \(2{e^{\frac{1}{4}\pi i}}\) | \({2^2}{e^{\frac{2}{4}\pi i}} = 4i\) | \({2^3}{e^{\frac{3}{4}\pi i}} = 8{e^{\frac{3}{4}\pi i}}\) | \({2^6}{e^{\frac{6}{4}\pi i}} = – 64i\) | \({2^8}{e^{\frac{8}{4}\pi i}} = {2^8}{e^{2\pi i}} = 256\) |
La Fórmula de Moivre e identidades trigonométricas
Como:
\(\left( {\cos \theta + i{\rm{sen}}\theta } \right) = {e^{i\theta }}\)
Entonces tenemos que:
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^k} = {\left( {{e^{i\theta }}} \right)^k} = {e^{ik\theta }} = \cos \left( {k\theta } \right) + i{\rm{sen}}\left( {k\theta } \right)\)
La Fórmula de Moivre establece:
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^k} = \cos \left( {k\theta } \right) + i{\rm{sen}}\left( {k\theta } \right)\)
Al desarrollar:
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^2} = {\cos ^2}\theta + 2i\cos \theta {\rm{sen}}\theta + {i^2}{\rm{se}}{{\rm{n}}^2}\theta = {\cos ^2}\theta – {\rm{se}}{{\rm{n}}^2}\theta + 2i\cos \theta {\rm{sen}}\theta \)
También
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^2} = \cos 2\theta + i{\rm{sen}}2\theta = {\cos ^2}\theta – {\rm{se}}{{\rm{n}}^2}\theta + i(2\cos \theta \;{\rm{sen}}\theta )\;\)
De lo anterior se deduce las identidades trigonométricas:
\(\cos 2\theta = {\cos ^2}\theta – {\rm{se}}{{\rm{n}}^2}\theta ,\;\;{\rm{sen}}2\theta = 2\cos \theta {\rm{sen}}\theta \)
Al desarrollar:
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^3} = {\cos ^3}\theta + 3{\cos ^2}\theta \left( {i{\rm{sen}}\theta } \right) + 3\cos \theta \left( {{i^2}{\rm{se}}{{\rm{n}}^2}\theta } \right) + \left( {{i^3}{\rm{se}}{{\rm{n}}^3}\theta } \right)\)\( = {\cos ^3}\theta – 3\cos \theta {\rm{se}}{{\rm{n}}^2}\theta + \left( {3{{\cos }^2}\theta {\rm{sen}}\theta – {\rm{se}}{{\rm{n}}^3}\theta } \right)i\)
Al aplicar la fórmula de Moivre para \(k = 3\):
\({\left( {\cos \theta + i{\rm{sen}}\theta } \right)^3} = \cos 3\theta + i{\rm{sen}}3\theta \)
Por lo cual obtenemos las siguientes identidades trigonométricas:
\(\cos 3\theta = {\cos ^3}\theta – 3\cos \theta {\rm{se}}{{\rm{n}}^2}\theta ,\;\;\sin 3\theta = 3{\cos ^2}\theta \sin \theta – {\rm{se}}{{\rm{n}}^3}\theta \)

Art. actualizado: Nov. 2022; sobre el original de diciembre, 2013.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.