Definición de Función Cuadrática

Maestría en Matemáticas, Dr. en Ciencias
Una función cuadrática de una variable real cuya forma se expresa
\(f\left( x \right) = a{x^2} + bx + c\)
Donde la variable es \(x\), \(a,b\) y c son constantes reales, llamadas coeficientes de la función cuadrática con \(a \ne 0.\)
En la tabla se avanza sobre ejemplos generales de funciones cuadráticas y la situación que pueden modelar, para luego ilustrar su aplicación directa a partir de problemas reales.
| Función cuadrática | Situación que puede modelar |
|---|---|
| \(f\left( x \right) = {x^2}\) | La variable \(y\) es el área de un cuadrado cuyo lado mide \(x\). |
| \(f\left( x \right) = \pi {x^2}\) | La variable \(y\) es el área de un círculo cuyo radio mide \(x\). |
| \(f\left( x \right) = 100 – 4.9{x^2}\) | La variable \(y\) es la altura de un objeto que fue soltado a una altura de 100 y \(x\) es el tiempo transcurrido. |
| \(f\left( x \right) = 60\left( {{\bf{sen}}45^\circ } \right)x – 4.9{x^2}\) | La variable \(y\) es la altura de una bala de cañón lanzada con un ángulo de 45° con una velocidad de 60 m/s y \(x\) es el tiempo transcurrido. |
La fórmula general y la función cuadrática
Si para \(x = \alpha \) la función cuadrática vale cero, entonces el número es \(\alpha \) es llamada raíz de la función cuadrática, si decir si, \(\alpha \) es solución de la ecuación cuadrática
\(a{x^2} + bx + c = 0\)
La fórmula general para resolver ecuaciones cuadráticas tenemos que las raíces de una función cuadrática son:
\(\alpha = \frac{{ – b + \sqrt {{b^2} – 4ac} }}{{2a}},\;\;\beta = \frac{{ – b – \sqrt {{b^2} – 4ac} }}{{2a}}\)
A partir de lo anterior se establece la siguiente relación entre las raíces y los coeficientes de la función cuadrática:
\(\alpha + \beta = – \frac{b}{a},\;\;\alpha \beta = \frac{c}{a}\)
Mediante productos notables se establece la siguiente identidad:
\(a{x^2} + bx + c = a\left( {x – \alpha } \right)\left( {x – \beta } \right)\)
De una manera similar a la que se establece la fórmula general se establece que la función cuadrática se puede expresar de la forma:
\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)
Con \(h = – \frac{b}{{2a}}\) y \(k = – \frac{{{b^2} – 4ac}}{a}\)
Al resolver la ecuación:
\(a{\left( {x – h} \right)^2} + k = 0\)
Se obtiene:
\(\left| {x – h} \right| = \sqrt { – \frac{k}{a}} \)
\(x = h \pm \sqrt { – \frac{k}{a}} \)
De lo anterior se concluye que \(f\left( x \right) = a{\left( {x – h} \right)^2} + k\), sólo en caso de que las constantes \(k\) y \(a\) son de signos contrarios, esta función cuadrática tiene raíces reales, las cuales son: \(h + \sqrt { – \frac{k}{a}} ,\;\;h – \sqrt { – \frac{k}{a}} \).
En caso de que las constantes \(k\) y \(a\) sean del mismo signo entonces la función cuadrática no tiene raíces reales.
Cuando \(k = 0,\;\;\)la función cuadrática sólo tiene una raíz.
Ejemplos aplicados sobre la vida real
Ejemplo de aplicación 1: Economía
Una escuela desea organizar un torneo de futbol donde cada equipo juegue contra cada uno de los otros equipos una sola vez. Se tiene un presupuesto de $15600 para el costo del arbitraje, si el costo de éste es de $200 por partido. ¿Cuántos equipos se pueden inscribir al torneo?
Planteamiento del problema: Debemos encontrar una función que calcule el número de partidos cuando se tienen \(n\) equipos para contarlos haremos la suposición que el equipo 1, juega primero con todos los demás, es decir \(n – 1\) partidos. El equipo 2 jugaría ahora con todos los restantes, es decir, con \(n – 2\), pues ya habrá jugado con el equipo 1. El equipo 3 ya habrá jugado con el equipo 1 y 2, entonces le restaría jugar con n-3 equipos.
Con el anterior razonamiento llegamos a:
\(f\left( n \right) = n – 1 + n – 2 + \ldots + 2 + 1\)
\(f\left( n \right) = \frac{{n\left( {n – 1} \right)}}{2}\)
La función de costo es:
\(C\left( n \right) = 200f\left( n \right) = 100n\left( {n – 1} \right)\)
Al tener $15600 de presupuesto, se tiene la ecuación:
\(100n\left( {n – 1} \right) = 15600\)
Solución de la ecuación
\(100n\left( {n – 1} \right) = 15600\) Situación inicial
\(n\left( {n – 1} \right) = 156\) Se dividió entre 100 cada lado de la ecuación
\({n^2} – n – 156 = \) Se sumó \( – 156\) a cada lado de la ecuación
\(\left( {n – 13} \right)\left( {n + 12} \right) = 0\) Se tiene \(\left( { – 13} \right)\left( {12} \right) = – 156\) y \( – 13 + 12 = – 1\)
Se factorizó.
Soluciones de la ecuación \(n = – 12,\;13\)
Respuesta: El presupuesto alcanza para que se inscriban 13 equipos.
Ejemplo de aplicación 2: Economía
Una compañía de autobuses de transporte metropolitano ha observado que, en una jornada de ocho horas, cada uno de sus autobuses transporta en promedio a mil pasajeros. Para estar en condiciones de dar un aumento salarial a sus trabajadores, tendrá que aumentar el costo del pasaje, que actualmente es de $5; un economista calcula que, por cada peso que aumente el pasaje, cada camión perderá en promedio 40 pasajeros en cada jornada. La compañía ha calculado que, para cubrir el aumento salarial, debe obtener en cada jornada $760 más por camión, ¿cuánto debe aumentar el pasaje?
Planteamiento del problema: Sea \(x\) la cantidad de pesos en que subirá el pasaje, por lo cual \(5 + x\) es el nuevo costo el pasaje. Con este mismo aumento cada camión transportará \(1000 – 40x\) pasajeros al día, en promedio.
Finalmente, el ingreso por camión es:
\(I\left( x \right) = \left( {5 + x} \right)\left( {1000 – 40x} \right) = – 40\left( {x + 5} \right)\left( {x – 25} \right)\)
Para poder cubrir el aumento salarial cada autobús debe de recabar: \(1000\left( 5 \right) + 760 = 5760\)
Finalmente se tiene la ecuación:
\( – 40\left( {x + 5} \right)\left( {x – 25} \right) = 5760\)
Solución de la ecuación
\( – 40\left( {x + 5} \right)\left( {x – 25} \right) = 5760\) Situación inicial
\(\left( {x + 5} \right)\left( {x – 25} \right) = – 144\) Se dividió entre \( – 40\) cada lado de la ecuación
\({n^2} – 20n – 125 = – 144\) Se desarrolló el producto notable
\({n^2} – 20n + 19 = 0\) Se sumó 144 a cada
\(\left( {n – 19} \right)\left( {n – 1} \right) = 0\) Se tiene \(\left( { – 19} \right)\left( { – 1} \right) = 19\) y \( – 19 – 1 = – 20\)
Se factorizó
Soluciones de la ecuación \(n = 1,19\)
Respuesta: El precio del pasaje puede subir $1 o $19 pesos.
Ejemplo de aplicación 3: Economía
Un expendio de pan vende un promedio de 1200 panecillos a la semana a $6 cada uno. Un día decidió aumentar el precio a $9 por pieza; ahora sus ventas han disminuido: sólo vende en promedio 750 panecillos a la semana. ¿Cuál debe ser el precio de cada panecillo para que los ingresos del expendio sean los mayores posibles? Suponga que existe una relación lineal entre la demanda y el precio.
Planteamiento del problema: Al asumir que hay una relación lineal entre la demanda D y el precio \(x,\) entonces
\(D = mx + b\)
Cuando \(x = 6;D = 1200;\;\) lo cual genera la ecuación:
\(1200 = 6m + b\)
Cuando \(x = 9;D = 750;\;\) lo y se obtiene la ecuación:
\(750 = 9m + b\)
Al resolver el sistema de ecuaciones, la relación entre la demanda y el precio es:
\(D = – 150x + 2100 = – 150\left( {x – 14} \right)\)
El ingreso es igual a
\(I\left( x \right) = Dx = – 150x\left( {x – 14} \right)\)
Solución
La gráfica del ingreso en una parábola que abre hacia abajo y su valor máximo se alcanza en el vértice el cual se puede encontrar calculando el promedio de las raíces de la función cuadrática que modela al ingreso. Las raíces son \(\alpha = 0,\;\;\beta = 14\).
\(h = \frac{{0 + 14}}{2} = 7\)
\(I\left( h \right) = – 150\left( 7 \right)\left( {7 – 14} \right) = 7350\)
Respuesta
El ingreso máximo es de $7350 y se logra con un precio de $7; vendiendo, en promedio 1050 panecillos a la semana.
Ejemplo de aplicación 4: Economía
El costo por fabricar \(n\) sillas en un día se puede calcular con la función cuadrática:
\(C\left( n \right) = {n^2} – 200n + 13000\)
Determinar el costo mínimo que se puede alcanzar.
Planteamiento del problema
La gráfica de \(C\left( n \right)\) es una parábola que abre hacia arriba y alcanzará su punto mínimo en \(h = – \frac{b}{{2a}} = – \frac{{\left( { – 200} \right)}}{{2\left( 1 \right)}} = 100\)
\(C\left( {100} \right) = {\left( {100} \right)^2} – 200\left( {100} \right) + 13000 = 3000\)
Respuesta
El menor costo posible es igual a $3000 y se logra al fabricar 100 sillas.
Ejemplo de aplicación 5: Geometría
Un rombo tiene un área de 21 cm2; si la suma de las longitudes de sus diagonales es 17 cm, ¿cuánto mide cada diagonal del rombo?
Planteamiento del problema: El área de un rombo se calcula con:
\(A = \frac{{Dd}}{2}\)
Con \(D\) y \(d\) las longitudes de sus diagonales, además se sabe:
\(D + d = 7\)
\(D = 17 – d\)
Al sustituir se obtiene:
\(A = \frac{{\left( {17 – d} \right)d}}{2}\)
Finalmente se obtiene la ecuación
\(\frac{{\left( {17 – d} \right)d}}{2} = 21\)
Solución
\(\frac{{\left( {17 – d} \right)d}}{2} = 21\) Situación inicial
\(\left( {17 – d} \right)d = 42\) Se multiplicó por \( – 40\) cada lado de la ecuación
\({d^2} – 17d + 42 = 0\) Se desarrolló el producto.
\(\left( {d – 14} \right)\left( {d – 3} \right) = 0\) Se tiene \(\left( { – 14} \right)\left( { – 3} \right) = 42\) y \( – 14 – 3 = – 17\)
Se factorizó
Soluciones de la ecuación \(d = 3,14\)
Respuesta:
Las diagonales del rombo miden 14 cm y 3cm.
Ejemplo de aplicación 6: Geometría
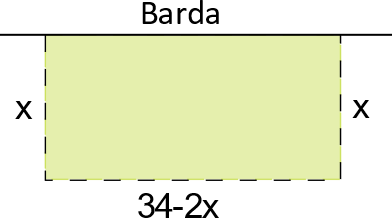
Se desea construir un gallinero rectangular de 140 m2, aprovechando una barda bastante larga que formará el fondo del gallinero. Los otros tres lados serán construidos con 34 metros lineales de malla de alambre, ¿cuánto deben medir el largo y el ancho del gallinero para usar el total de malla?
Bajo las mismas condiciones ¿Cuál es el área máxima que se puede cercar con la misma malla?
Planteamiento del Problema: De acuerdo con el esquema el área es igual a:
\(A\left( x \right) = x\left( {34 – 2x} \right) = 2x\left( {17 – x} \right)\)
Donde \(x\) es la longitud del lado perpendicular a la barda.
Para saber las medidas del rectángulo para que tenga un área de140 m2 basta con resolver la ecuación
\(2x\left( {17 – x} \right) = 140\)
Como la gráfica de \(A\left( x \right)\) es una parábola que abre hacia abajo para calcular el máximo valor del área es suficiente con calcular el vértice de la parábola.
Respuestas
Medidas del rectángulo con área 140 m2
Longitud del lado perpendicular a la barda
\(x\) Longitud del lado paralela a la barda
\(34 – 2x\)
10 14
7 20
La primera coordenada del vértice es \(h = \frac{{17}}{2}\) y
\(A\left( h \right) = \frac{{289}}{2}\)
El área se máxima cuando el lado perpendicular mide \(\frac{{17}}{2}\;\)m y el lado paralelo mide 17mlelo mide 17m el valor del área máxima alcanzada es de \(\frac{{289}}{2}\)m2.
Gráfica de una función cuadrática
Desde un punto de vista geométrica, las raíces son los puntos donde la gráfica de una función intersecta al eje de las \(x\).
A partir de la expresión
\(f\left( x \right) = a{\left( {x – h} \right)^2} + k,\)
estableceremos la forma general de la gráfica de una función cuadrática.
Primer caso \(a > 0\) y \(k > 0\)
\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)
| \(x\) | \(f\left( x \right)\) |
|---|---|
| \(h – 1\) | \(a + k\) |
| \(h – 2\) | \(4a + k\) |
| \(h – 3\) | \(9a + k\) |
| \(h – 4\) | \(16a + k\) |
| \(h\) | \(k\) |
| \(h + 1\) | \(a + k\) |
| \(h + 2\) | \(4a + k\) |
| \(h + 3\) | \(9a + k\) |
| \(h + 4\) | \(16a + k\) |
En este caso la gráfica satisface:
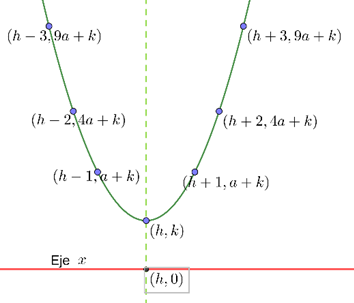
Simétrica: Con eje de simetría \(x = h = – \frac{b}{{2a}}.\) Es decir \(f\left( {h – s} \right) = f\left( {h + s} \right)\)
Está por encima del eje de las \(x\) y no lo intersecta. Es decir \(f\left( x \right) > 0\) no tiene raíces reales.
El punto más bajo de la gráfica es en el punto \(\left( {h,k} \right)\). Es decir \(f\left( x \right) \ge f\left( h \right) = k\)
Segundo caso \(a < 0\) y \(k < 0\)
\(f\left( x \right) = a{\left( {x – h} \right)^2} + k\)
| \(x\) | \(f\left( x \right)\) |
|---|---|
| \(h – 1\) | \(a + k\) |
| \(h – 2\) | \(4a + k\) |
| \(h – 3\) | \(9a + k\) |
| \(h – 4\) | \(16a + k\) |
| \(h\) | \(k\) |
| \(h + 1\) | \(4a + k\) |
| \(h + 2\) | \(9a + k\) |
| \(h + 3\) | \(4a + k\) |
| \(h + 4\) | \(16a + k\) |
En este caso la gráfica satisface:
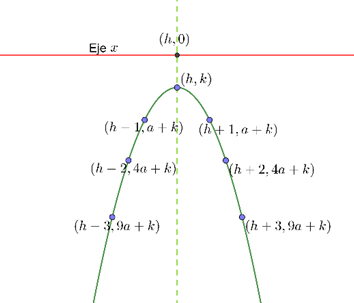
Simétrica: Con eje de simetría \(x = h = – \frac{b}{{2a}}.\) Es decir \(f\left( {h – s} \right) = f\left( {h + s} \right)\)
Está por debajo del eje de las \(x\) y no lo intersecta. Es decir \(f\left( x \right) < 0\) no tiene raíces reales. El punto más alto de la gráfica es en el punto \(\left( {h,k} \right)\). Es decir \(f\left( x \right) \le f\left( h \right) = k\) Tercer caso \(a > 0\) y \(k \le 0\).
Este caso es similar al primer caso la diferencia estriba en que ahora se tienen una raíz real (cuando \(k = 0\) ) o dos raíces reales.
En este caso la gráfica satisface:
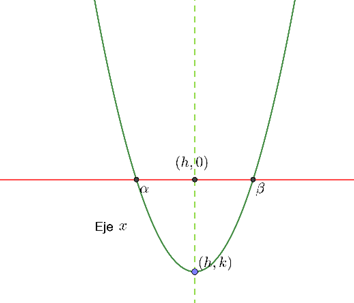
Simétrica: Con eje de simetría \(x = h = – \frac{b}{{2a}}.\) Es decir \(f\left( {h – s} \right) = f\left( {h + s} \right)\)
Intersecta al eje de las \(x\), es decir al menos tiene una raíz real.
El punto más bajo de la gráfica es en el punto \(\left( {h,k} \right)\). Es decir \(f\left( x \right) \ge f\left( h \right) = k\)
Cuarto caso \(a < 0\) y \(k \ge 0\).
Este caso es similar al segundo caso la diferencia estriba en que ahora se tienen una raíz real (cuando \(k = 0\) ) o dos raíces reales.
En este caso la gráfica satisface:
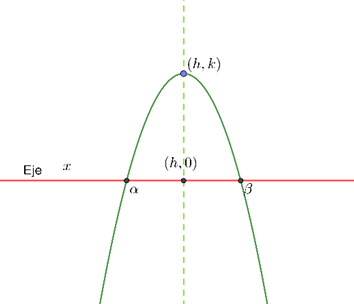
Simétrica: Con eje de simetría \(x = h = – \frac{b}{{2a}}.\) Es decir \(f\left( {h – s} \right) = f\left( {h + s} \right)\)
El punto más bajo de la gráfica es en el punto \(\left( {h,k} \right)\). Es decir \(f\left( x \right) \le f\left( h \right) = k\)
La gráfica de una función cuadrática es llamada parábola y sus elementos a destacar son el eje de simetría, los puntos donde intersecta al eje de las \(x\) y el vértice, que es el punto de la gráfica de la función donde alcanza su punto más bajo o alto dependiendo del caso.
Por el análisis realizado podemos afirmar:
La parábola asociada con la función cuadrática \(f\left( x \right) = a{x^2} + bx + c\) tiene su vértice en \(\left( {h,k} \right)\) donde:
\(h = – \frac{b}{{2a}},\;\;k = f\left( h \right)\)
Ejemplos
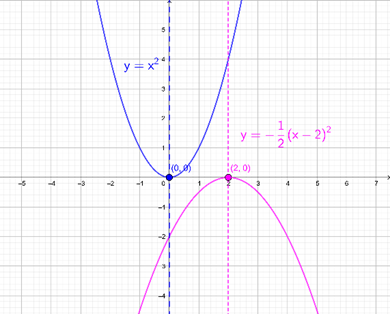
| Función cuadrática \(y = {x^2}\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( {0,0} \right)\) |
| Eje de simetría de la parábola | \(x = 0\) |
| Intersecciones con el eje \(x\) | \(\left( {0,0} \right)\) |
| Función cuadrática \(y = – \frac{1}{2}{\left( {x – 2} \right)^2}\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( {2,0} \right)\) |
| Eje de simetría de la parábola | \(x = 2\) |
| Intersecciones con el eje \(x\) | \(\left( {2,0} \right)\) |
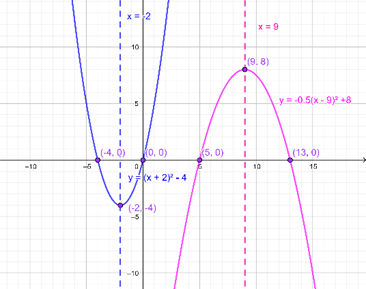
| Función cuadrática \(y = {\left( {x + 2} \right)^2} – 4\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( { – 2, – 4} \right)\) |
| Eje de simetría de la parábola | \(x = – 2\) |
| Intersecciones con el eje \(x\) | \(\left( { – 4,0} \right);\left( {0,0} \right)\) |
| Función cuadrática \(y = – \frac{1}{2}{\left( {x – 9} \right)^2} + 8\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( {9,8} \right)\) |
| Eje de simetría de la parábola | \(x = 9\) |
| Intersecciones con el eje \(x\) | \(\left( {5,0} \right);\left( {13,0} \right)\) |
| Función cuadrática \(y = {x^2} + 1\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( {0,1} \right)\) |
| Eje de simetría de la parábola | \(x = 0\) |
| Intersecciones con el eje \(x\) | No tiene |
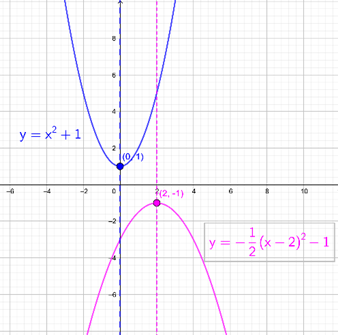
| Función cuadrática \(y = – \frac{1}{2}{\left( {x – 2} \right)^2} – 1\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( {2, – 1} \right)\) |
| Eje de simetría de la parábola | \(x = 2\) |
| Intersecciones con el eje \(x\) | No tiene |
En caso de existir las raíces reales de una función cuadrática, podemos graficar su parábola asociada a partir de ellas. Supongamos que \(f\left( x \right) = a\left( {x – \alpha } \right)\left( {x – \beta } \right)\)
Para ello hay que tener en cuenta lo siguiente:
\(\alpha + \beta = – \frac{b}{a}\)
\(\frac{{\alpha + \beta }}{2} = – \frac{b}{{2a}} = h\)
Como
\(k = f\left( h \right)\)
\(k = f\left( {\frac{{\alpha + \beta }}{2}} \right)\)
\(k = a\left( {\frac{{\alpha + \beta }}{2} – \alpha } \right)\left( {\frac{{\alpha + \beta }}{2} – \beta } \right)\)
\(k = – \frac{a}{4}{\left( {\alpha – \beta } \right)^2}\)
Ejemplos
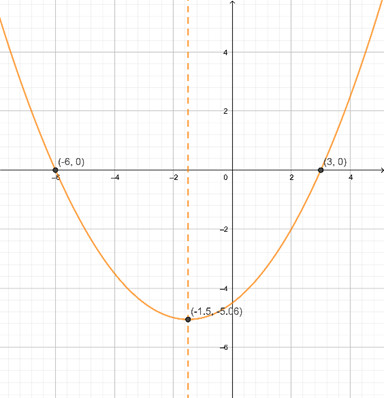
Hacer el esbozo de la gráfica de la función cuadrática \(f\left( x \right) = \frac{1}{4}\left( {x – 3} \right)\left( {x + 6} \right)\)
Solución
Las raíces son \(\alpha = 3\;\) y \(\beta = – 6\); entonces \(h = \frac{{3 – 6}}{2} = – \frac{3}{2}\).
\(k = f\left( { – \frac{3}{2}} \right) = 2\left( { – \frac{3}{2} – 3} \right)\left( { – \frac{3}{2} + 6} \right) = \frac{1}{4}\left( { – \frac{9}{2}} \right)\left( {\frac{9}{2}} \right) = – \frac{{81}}{{16}}\)
Por lo cual podemos construir la siguiente tabla
| \(f\left( x \right) = 2\left( {x – 3} \right)\left( {x + 6} \right)\) | Elementos importantes |
|---|---|
| Vértice de la parábola | \(\left( { – \frac{3}{2}, – \frac{{81}}{2}} \right)\) |
| Eje de simetría de la parábola | \(x = – \frac{{81}}{2}\) |
| Intersecciones con el eje \(x\) | \(\left( { – 6,0} \right)\;,\;\left( {3,0} \right)\) |
Para hacer un esbozo de la gráfica de la función:
\(f\left( x \right) = 3{x^2} – 18x + 4\)
Usaremos las mismas ideas que ya hemos, usado; para ello primero determinaremos el vértice.
En este caso, \(a = 3;b = – 12,\;c = 4\).
Como \(a > 0\), la parábola “abrirá hacia arriba y \(h = – \frac{b}{{2a}} = – \left( {\frac{{ – 18}}{{3\left( 2 \right)}}} \right) = 3.\) A continuación calcularemos \(k:\)
\(k = f\left( h \right) = f\left( 3 \right) = 3{\left( 3 \right)^2} – 18\left( 3 \right) + 4 = – 23\)
El vértice de la parábola está en \(\left( {3, – 23} \right)\) y como abre hacia arriba, entonces la parábola intersectará a l eje de las \(x\;\)y su eje de simetría es \(x = 3\).
Ahora consideremos a la función cuadrática
\(f\left( x \right) = – 5{x^2} + 10x – 9\)
En este caso, \(a = 3;b = – 12,\;c = 4\).
Como \(a < 0\), la parábola “abrirá “hacia abajo y \(h = - \frac{b}{{2a}} = - \left( {\frac{{10}}{{\left( 2 \right)\left( { - 5} \right)}}} \right) = 1.\) A continuación calcularemos \(k:\) \(k = f\left( h \right) = f\left( 1 \right) = - 5{\left( 1 \right)^2} + 10\left( 1 \right) - 9 = - 4\) El vértice de la parábola está en \(\left( {1, - 4} \right)\) y como abre hacia abajo, entonces la parábola no intersectará al eje de las \(x\;\)y su eje de simetría es \(x = 1.\)

Trabajo publicado en: Nov., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.