Definición de Fracciones Mixtas, Unitarias, Homogéneas y Heterogéneas

Maestría en Matemáticas, Dr. en Ciencias
Mixtas. Una fracción mixta se compone de un número entero mayor o igual que uno y una fracción propia, la escritura general de una fracción mixta es de la forma: \(a + \frac{c}{d},\) cuya escritura compacta es: \(a\frac{c}{d},\;\), es decir: \(a\frac{c}{d} = a + \frac{c}{d}\). El número \(a\) es llamada la parte entera de la fracción mixta y \(\frac{c}{d}\) es llamada su parte fraccionaria.
Homogéneas. Si dos o más fracciones tienen el mismo denominador, se dice que estas son fracciones homogéneas. Por ejemplo, las fracciones \(\frac{3}{4},\) \(\frac{7}{4},\) \(\frac{1}{4},\) \(\frac{{10}}{4}\) son homogéneas porque todas tienen el mismo denominador, que en este caso es el \(4\). Mientras que las fracciones \(\frac{3}{4},\) \(\frac{7}{4},\) \(\frac{1}{4},\) \(\frac{5}{2}\) no son fracciones homogéneas pues el denominador de \(\frac{5}{2}\) es \(2\) y el denominador de las demás fracciones es \(4\). Una de las ventajas de las fracciones homogéneas es que las operaciones aritméticas de suma y resta de funciones, es muy sencilla.
Heterogéneas. Si dos o más fracciones al menos dos de ellas no tienen el mismo denominador entonces se dice que estas fracciones son fracciones heterogéneas. Las siguientes fracciones son heterogéneas: \(\frac{3}{5},\;\) \(\frac{7}{5}\), \(\frac{1}{4},\) \(\frac{2}{5}\).
Unitarias. Una fracción se identifica como unitaria si el numerador es igual a 1 \(1,\) \(2\) . Las siguientes fracciones son ejemplos de fracciones unitarias: \(\frac{1}{2},\;\) \(\frac{1}{3}\), \(\frac{1}{4}\),\(\;\frac{1}{5}\).
Expresión verbal de una fracción mixta
| Fracción mixta | Expresión verbal |
|---|---|
| \(3\frac{1}{2} = \) | Tres enteros y medio |
| \(5\frac{3}{4} = \) | Cinco enteros y tres cuartos |
| \(10\frac{1}{8} = \) | Diez enteros con un octavo |
Conversión de una fracción mixta a una fracción impropia
Las fracciones mixtas son útiles para realizar estimaciones, por ejemplo, es fácil establecer:
\(5\frac{1}{{20}} > 4\frac{9}{{10}}\)
Sin embargo, las fracciones mixtas, suelen ser poco practicas para realizar operaciones como la multiplicación y la división, es por ello que es importante como convertir a una fracción mixta
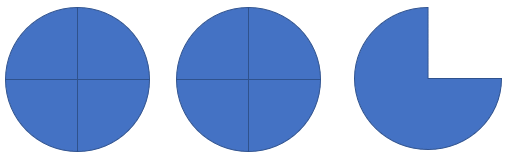
La figura anterior representa a la fracción mixta \(2\frac{3}{4}\), ahora cada entero está compuesto por cuatro cuartos por lo cual en 2 enteros hay 8 cuartos y a estos hay que sumar los otros 3 cuartos, es decir:
\(2\frac{3}{4} = \frac{{2\left( 4 \right) + 3}}{4} = \frac{{11}}{4}\)
De manera general:
\(a\frac{c}{d} = \frac{{ad + c}}{d}\)
La tabla siguiente muestra otros ejemplos.
| Fracción mixta | Operaciones a realizar | Fracción impropia |
|---|---|---|
| \(3\frac{1}{2}\) | \(\frac{{3\left( 2 \right) + 1}}{2}\) | \(\frac{7}{2}\) |
| \(5\frac{3}{4}\) | \(\frac{{5\left( 4 \right) + 3}}{4}\) | \(\frac{{23}}{4}\) |
| \(10\frac{1}{8}\) | \(\frac{{10\left( 8 \right) + 1}}{8}\) | \(\frac{{81}}{8}\) |
Conversión de una fracción impropia a una fracción mixta
Para convertir una fracción impropia a una fracción mixta se calcula el cociente y el residuo de dividir el numerador entre el denominador. El cociente obtenido será la parte entera de la fracción mixta y la fracción propia será \(\frac{{{\rm{residuo}}}}{{{\rm{denominador}}}}\)
Ejemplo
Para convertir \(\frac{{25}}{7}\) a una fracción mixta:
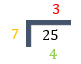
Por las operaciones realizados obtenemos:
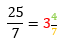
La tabla siguiente muestra otros ejemplos
| Fracción impropia | Cálculo del cociente y del residuo | Fracción impropia |
|---|---|---|
| \(\frac{{25}}{7}\) |
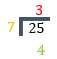 |
\(3\frac{4}{7}\) |
| \(\frac{{35}}{8}\) |
 |
\(4\frac{3}{8}\) |
| \(\frac{{46}}{5}\) |
 |
\(9\frac{1}{5}\) |
Uso cotidiano de las fracciones mixtas y propias
En la vida cotidiana necesitamos medir, comprar, comparar precios, nos ofrezcan descuentos; para medir necesitamos unidades de medida y no siempre ofrecen unidades enteras de los productos y no siempre se paga con una cantidad entera de monedas de una unidad.
Por ejemplo, es común que ciertos líquidos los vendan en envases cuyo contenido sea \(\frac{3}{4}\;\)de litro, medio galón o galón y medio. Quizá cuando vayas a comprar un tubo pidas de \(\frac{1}{8},\;\) \(\frac{7}{8},{\rm{\;}}\) \({\rm{3}}\frac{1}{2}\) y no sea necesario que digas la unidad de medida, que en este caso es la pulgada.
Operaciones básicas de fracciones homogéneas
La suma de \(\frac{3}{4}\) y \(\frac{2}{4}\), se ejemplifica en el siguiente esquema:

\(\frac{3}{4} + \frac{2}{4} = \frac{{3 + 2}}{4} = \frac{5}{4}\)
Mientras que la resta se realiza de la siguiente manera:
\(\frac{3}{4} – \frac{2}{4} = \frac{{3 – 2}}{4} = \frac{1}{4}\)
De manera general, para fracciones homogéneas:
\(\frac{a}{d} + \frac{b}{d} = \frac{{a + b}}{d}\)
\(\frac{a}{d} – \frac{b}{d} = \frac{{a – b}}{d}\)
Los egipcios y las fracciones unitarias
La cultura egipcia logró un notable desarrollo tecnológico y esto no hubiese ocurrido sin un desarrollo a la par de las matemáticas. Existen vestigios históricos donde se pueden encontrar registros del uso de las fracciones en la cultura egipcia, con una particularidad, ellos, sólo usaban fracciones unitarias.
Hay varios casos en que la escritura de una fracción como suma de fracciones unitarias es sencilla como
\(\frac{3}{n} = \frac{1}{n} + \frac{1}{{2n}}\)
En el caso de que \(n = 2q + 1\), es decir impar tenemos que:
\(\frac{2}{n} = \frac{1}{{q + 1}} + \frac{1}{{n\left( {q + 1} \right)}}\)
Lo anterior lo ilustraremos con dos ejemplos
Para expresar \(\frac{2}{{11}}\); en este caso se tiene \(11 = 2\left( 5 \right) + 1\), por lo tanto:
\(\frac{2}{{11}} = \frac{1}{6} + \frac{1}{{11\left( 6 \right)}},\)
es decir,
\(\frac{2}{{11}} = \frac{1}{6} + \frac{1}{{66}}\)
Para expresar \(\frac{2}{{17}}\); en este caso se tiene \(17 = 2\left( 8 \right) + 1\),
\(\frac{2}{{15}} = \frac{1}{8} + \frac{1}{{120}}\)
A continuación, mostramos algunas fracciones como suma de fracciones unitarias,
| Fracción | Expresión como suma de fracciones unitarias | Fracción | Expresión como suma de fracciones unitarias |
|---|---|---|---|
| \(\frac{3}{n}\) | \(\frac{1}{n} + \frac{1}{{2n}}\) | \(\frac{5}{8}\) | \(\frac{1}{2} + \frac{1}{8}\) |
| \(\frac{2}{3}\) | \(\frac{1}{2} + \frac{1}{6}\) | \(\frac{7}{8}\) | \(\frac{1}{2} + \frac{1}{4} + \frac{1}{8}\) |
| \(\frac{3}{4}\) | \(\frac{1}{2} + \frac{1}{4}\) | \(\frac{2}{9}\) | \(\frac{1}{5} + \frac{1}{{45}}\) |
| \(\frac{3}{5}\) | \(\frac{1}{5} + \frac{1}{{10}}\) | \(\frac{5}{9}\) | \(\frac{1}{2} + \frac{1}{{18}}\) |
| \(\frac{4}{5}\) | \(\frac{1}{2} + \frac{1}{4} + \frac{1}{{20}}\) | \(\frac{7}{9}\) | \(\frac{1}{2} + \frac{1}{4} + \frac{1}{{36}}\) |
| \(\frac{5}{6}\) | \(\frac{1}{2} + \frac{1}{3}\) | \(\frac{8}{9}\) | \(\frac{1}{2} + \frac{1}{3} + \frac{1}{{18}}\) |
| \(\frac{3}{7}\) | \(\frac{1}{3} + \frac{1}{{11}} + \frac{1}{{231}}\) | \(\frac{4}{9}\) | \(\frac{1}{3} + \frac{1}{9}\) |
| \(\frac{4}{7}\) | \(\frac{1}{2} + \frac{1}{{14}}\) | \(\frac{5}{9}\) | \(\frac{1}{2} + \frac{1}{{18}}\) |
| \(\frac{5}{7}\) | \(\frac{1}{2} + \frac{1}{5} + \frac{1}{{10}}\) | \(\frac{5}{9}\) | \(\frac{1}{2} + \frac{1}{{18}}\) |
| \(\frac{6}{7}\) | \(\frac{1}{2} + \frac{1}{3} + \frac{1}{{42}}\) | \(\frac{{19}}{{20}}\) | \(\frac{1}{2} + \frac{1}{4} + \frac{1}{5}\) |
Usando la tabla anterior podemos sumar fracciones y expresar tales sumas; como suma de fracciones unitarias.
Ejemplos de Fracciones heterogéneas
Ejemplo 1
\(\frac{2}{5} + \frac{4}{9} = \left( {\frac{1}{3} + \frac{1}{{15}}} \right) + \left( {\frac{1}{3} + \frac{1}{9}} \right)\)
\(\frac{2}{5} + \frac{4}{9} = \frac{2}{3} + \frac{1}{{15}} + \frac{1}{9}\)
\(\frac{2}{5} + \frac{4}{9} = \left( {\frac{1}{2} + \frac{1}{6}} \right) + \frac{1}{{15}} + \frac{1}{9}\)
Ejemplo 2
\(\frac{4}{7} + \frac{5}{9} = \left( {\frac{1}{2} + \frac{1}{{14}}} \right) + \left( {\frac{1}{2} + \frac{1}{{18}}} \right)\)
\(\frac{2}{7} + \frac{5}{9} = 1 + \frac{1}{{14}} + \frac{1}{{18}}\)
Finalmente podemos expresar a una misma fracción como suma de fracciones unitarias de diferente manera como:
\(\frac{8}{{63}} = \frac{1}{8} + \frac{1}{{504}}\)
\(\frac{8}{{63}} = \frac{1}{9} + \frac{1}{{63}}\)
\(\frac{8}{{63}} = \frac{1}{{14}} + \frac{1}{{18}}\)

Trabajo publicado en: Dic., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.