Definición de Fracciones Equivalentes

Maestría en Matemáticas, Dr. en Ciencias
Dos o más fracciones se dicen que son equivalentes si representan a la misma cantidad, es decir, si
\(\frac{a}{b} = \frac{c}{d}\;,\)
se dice que las fracciones \(\frac{a}{b}\) y \(\frac{c}{d}\) son equivalentes.
Fracciones equivalentes: representación gráfica
Consideremos al cuadrado, al cual lo dividiremos en cuartos, tercios, octavos y doceavos.
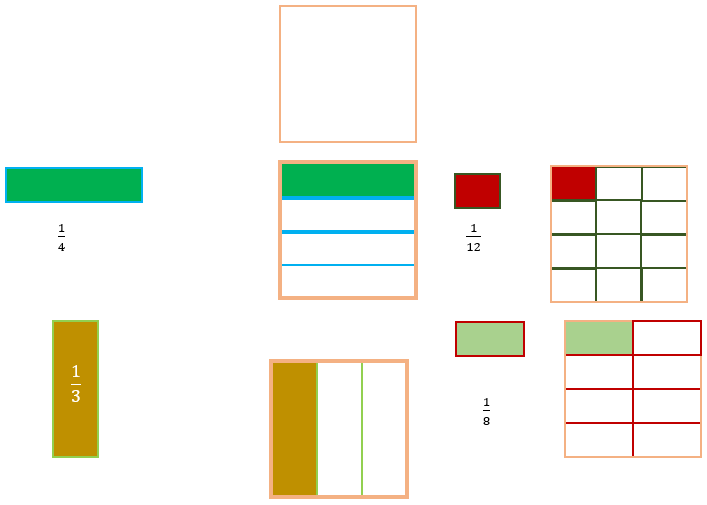
De las figuras anteriores nos percatamos de las siguientes equivalencias:
¿Cómo obtener una o varias fracciones equivalentes?
Existen dos métodos básicos para obtener una fracción equivalente a una fracción dada.
1. Se multiplica el numerador y el denominador por un mismo número positivo.
Ejemplos:
\(\frac{3}{4} = \frac{{3\left( 5 \right)}}{{4\left( 5 \right)}} = \frac{{15}}{{20}}\)
\(\frac{3}{4} = \frac{{3\left( 7 \right)}}{{4\left( 7 \right)}} = \frac{{21}}{{28}}\)
\(\frac{5}{8} = \frac{{5\left( 6 \right)}}{{8\left( 6 \right)}} = \frac{{30}}{{56}}\)
2. Se divide por un mismo divisor común positivo del numerador y del denominador.
\(\frac{{52}}{{56}} = \frac{{52 \div 4}}{{56 \div 4}} = \frac{{13}}{{14}}.\)
\(\frac{{80}}{{140}} = \frac{{80 \div 20}}{{140 \div 20}} = \frac{4}{7}.\)
\(\frac{{21}}{{57}} = \frac{{21 \div 3}}{{57 \div 3}} = \frac{7}{{19}}\)
Cuando en una fracción tanto el numerador como el denominador son divididos por un mismo divisor común distinto de 1, se dice que la fracción ha sido reducida.
Fracciones irreducibles
Una fracción se llama fracción irreducible si el máximo común divisor del numerador y del denominador es igual a 1.
Si \(mcd\left( {a,b} \right) = 1,\) la fracción \(\frac{a}{b}\) es llamada fracción irreducible.
Dada una fracción \(\frac{a}{b}\) para obtener una fracción equivalente a esta fracción y que además sea una fracción irreducible el numerador y numerador se divide entre el máximo común divisor de \(a\;\)y de \(b.\)
La siguiente tabla muestra ejemplos de fracciones irreducibles y reducibles; en caso de que sea reducible, se muestra como obtener una fracción equivalente irreducible.
| Fracción | Máximo común divisor | Irreducible | Fracción equivalente irreducible |
|---|---|---|---|
| \(\frac{{14}}{{42}}\) | 7 | No | \(\frac{{14}}{{42}} = \frac{{14 \div 7}}{{42 \div 7}} = \frac{2}{7}\) |
| \(\frac{3}{{25}}\) | 1 | Sí | \(\frac{3}{{25}}\) |
| \(\frac{{21}}{{201}}\) | 3 | No | \(\frac{{21 \div 3}}{{20\;1 \div 3}} = \frac{7}{{67}}\) |
| \(\frac{5}{{24}}\) | 1 | Sí | \(\frac{5}{{24}}\) |
| \(\frac{{72}}{{1125}}\) | 9 | No | \(\frac{{72}}{{1125}} = \frac{{72 \div 9}}{{1125 \div 9}} = \frac{8}{{125}}\) |
Fracciones equivalentes: representación verbal.
La siguiente tabla muestra dos maneras distintas de mostrar información equivalente, desde el punto de vista numérico.
| Frase verbal | Frase equivalente (numéricamente) | Argumentación |
|---|---|---|
| En 1930, en México, 4 personas de cada 25 personas hablaban una lengua originaria. | En 1930, en México, 16 personas de cada 100 personas hablaban una lengua originaria. | Ambos datos fueron multiplicados por 4 |
| En 1960, en México, 104 personas de cada 1000 personas hablaban una lengua originaria. | En 1960, en México, 13 personas de cada 125 personas hablaban una lengua originaria | Ambos datos fueron divididos entre 8. |
Fracciones equivalentes: representación decimal
La tabla siguiente muestra varios números decimales y fracciones equivalentes que lo representan.
| Número decimal | Fracción | Fracción equivalente | Operaciones |
|---|---|---|---|
| \(0.25\) | 0.25=\(\frac{{25}}{{100}}\) | 0.25=\(\frac{1}{4}\) | \(25 \div 25 = 1\) \(100 \div 25 = \) |
| \(1.4\) | \(1.4 = 1 + \frac{4}{{10}} = \frac{{14}}{{10}}\) | \(1.4 = \frac{7}{5}\) | \(14 \div 2 = 1\) \(10 \div 2 = 5\) |
| \(0.145\) | \(0.145 = \frac{{145}}{{1000}}\) | \(0.145 = \frac{{29}}{{200}}\) | \(145 \div 5 = 29\) \(1000 \div 5 = 200\) |
Fracciones equivalentes: representación como porcentaje
La tabla siguiente muestra varios números decimales y fracciones equivalentes que lo representan.
| Número decimal | Fracción | Fracción equivalente | Operaciones |
|---|---|---|---|
| 20% | \(\frac{{20}}{{100}}\) | \(\frac{1}{5}\) | \(20 \div 20 = 1\) \(100 \div 20 = 5\) |
| 150% | \(\frac{{150}}{{100}}\) | \(\frac{3}{2}\) | \(150 \div 50 = 3\) \(100 \div 50 = 2\) |
| 55% | \(\frac{{55}}{{100}}\) | \(\frac{{11}}{{20}}\) | \(55 \div 11 = 5\) \(100 \div 5 = 20\) |
Fracciones equivalentes: de heterogéneas a homogéneas
Dadas dos fracciones \(\frac{a}{b}\) y \(\frac{c}{d}\) , heterogéneas podemos encontrar dos fracciones homogéneas de tal manera, que una fracción sea equivalente a la fracción \(\frac{a}{b}\;\)y la otra a \(\frac{c}{d}\).
A continuación, mostraremos dos procedimientos para realizar lo que se menciona en el párrafo anterior.
Observemos:
\(\frac{a}{b} = \frac{{a\left( d \right)}}{{b\left( d \right)}}\)
\(\frac{c}{d} = {\rm{\;}}\frac{{c\left( b \right)}}{{d\left( b \right)}}\)
La siguiente tabla muestra algunos ejemplos.
| F. heterogéneas | Operaciones | F. homogéneas |
|---|---|---|
| \(\frac{4}{5}\), \(\frac{2}{3}\) | \(\frac{{4\left( 3 \right)}}{{5\left( 3 \right)}} = \frac{{12}}{{15}}\) \(\frac{{2\left( 5 \right)}}{{3\left( 5 \right)}} = \frac{{10}}{{15}}\) |
\(\frac{{12}}{{15}}\), \(\frac{{10}}{{15}}\) |
| \(\frac{7}{{12}}\), \(\frac{4}{{18}}\) | \(\frac{{7\left( {18} \right)}}{{12\left( {18} \right)}} = \frac{{126}}{{216}}\) \(\frac{{4\left( {12} \right)}}{{18\left( {12} \right)}} = \frac{{48}}{{216}}\) |
\(\frac{{126}}{{216}},\) \(\frac{{48}}{{216}}\) |
| \(\frac{7}{{10}}\), \(\frac{3}{{14}}\), \(\frac{5}{4}\) | \(\frac{{7\left( {14} \right)\left( 4 \right)}}{{10\left( {14} \right)4}} = \frac{{392}}{{560}}\) \(\frac{{3\left( {10} \right)\left( 4 \right)}}{{14\left( {10} \right)\left( 4 \right)}} = \frac{{120}}{{560}}\) \(\frac{{5\left( {10} \right)\left( {14} \right)}}{{4\left( {10} \right)\left( {14} \right)}} = \frac{{700}}{{560}}\) |
\(\frac{{392}}{{560}}\), \(\frac{{120}}{{560}},\) \(\frac{{700}}{{560}}\) |
La desventaja de este método es que en el proceso pueden salir números muy grandes; en muchas ocasiones es posible evitarlo, si se calcula el mínimo común múltiplo de los denominadores y el segundo método es con base en el cálculo del mínimo común múltiplo.
Mínimo común múltiplo en el cálculo de fracciones
A continuación, mediante dos ejemplos, como obtener fracciones homogéneas usando el mínimo común múltiplo delos denominadores, que será el denominador común de las fracciones involucradas.
Consideremos a las fracciones: \(\frac{7}{{12}}\), \(\frac{4}{{18}}.\)
El mínimo común múltiplo de \(12\) y \(18\) es \(36\); ahora
\(36 \div 12 = 3\)
\(36 \div 18 = 2\)
\(\frac{7}{{12}} = \frac{{7\left( 3 \right)}}{{12\left( 3 \right)}} = \frac{{21}}{{36}},\)
\(\frac{4}{{18}} = \frac{{4\left( 2 \right)}}{{18\left( 2 \right)}} = \frac{8}{{36}}\)
Ahora consideremos a las fracciones: \(\frac{7}{{10}}\), \(\frac{3}{{14}}\), \(\frac{5}{4}\)
El mínimo común múltiplo de \(10\), \(14\) y \(3\) es \(140\); ahora
\(140 \div 10 = 14\)
\(140 \div 14 = 10\)
\(140 \div 4 = 35\)
\(\frac{7}{{10}} = \frac{{7\left( {14} \right)}}{{10\left( {14} \right)}} = \frac{{98}}{{140}},\)
\(\frac{3}{{14}} = \frac{{3\left( {10} \right)}}{{14\left( {10} \right)}} = \frac{{30}}{{140}}\)
\(\frac{5}{4} = \frac{{5\left( {35} \right)}}{{4\left( {35} \right)}} = \frac{{175}}{{140}}\)
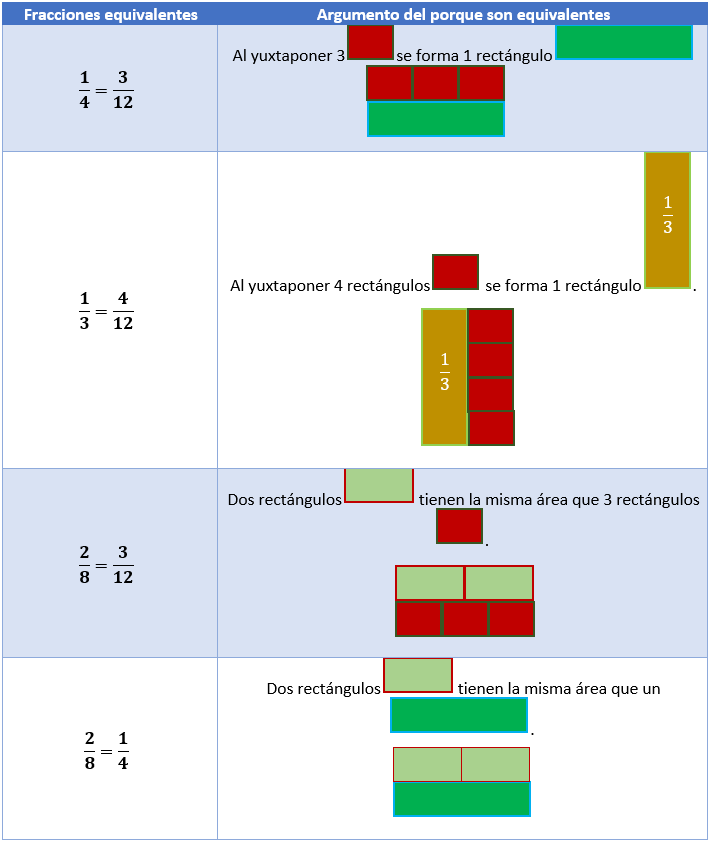
De las figuras anteriores nos percatamos del siguiente hecho:
\(\frac{1}{4} = \frac{3}{{12}}\)
A continuación, mostramos otros ejemplos.
| F. heterogéneas | Mín. común denominadores | Operaciones | F. homogéneas |
|---|---|---|---|
| \(\frac{1}{{14}}\) \(\frac{1}{{18}}\) | 126 | \(126 \div 14 = 9\) \(\frac{1}{{14}} = \frac{{1\left( 9 \right)}}{{14\left( 9 \right)}} = \frac{9}{{126}}\) \(126 \div 18 = 7\) \(\frac{1}{{18}} = \frac{{1\left( 7 \right)}}{{18\left( 7 \right)}} = \frac{7}{{126}}\) |
\(\frac{9}{{126}}\), \(\frac{7}{{126}}\) |
| \(\frac{5}{6}\) \(\frac{2}{{15}},\) \(\frac{4}{9}\) | 90 | \(90 \div 6 = 15\) \(\frac{5}{6} = \frac{{5\left( {15} \right)}}{{6\left( {15} \right)}} = \frac{{75}}{{90}}\) \(90 \div 15 = 6\) \(\frac{2}{{15}} = \frac{{2\left( {15} \right)}}{{15\left( 6 \right)}} = \frac{{30}}{{90}}\) \(90 \div 9 = 10\) \(\frac{4}{9} = \frac{{4\left( {10} \right)}}{{9\left( {10} \right)}} = \frac{{40}}{{90}}\) |
\(\frac{{75}}{{90}}\), \(\frac{{30}}{{90}}\), \(\frac{{40}}{{90}}\) |
Siga en Fracciones Equivalentes (parte 2)

Trabajo publicado en: Dic., 2022.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.