Evelyn Maitee Marín
Ingeniera Industrial, MSc en Física, y EdD

La flotabilidad se refiere a la capacidad de un fluido de ejercer una fuerza de empuje sobre un cuerpo que se encuentra total o parcialmente sumergido en el mismo. La flotabilidad a su vez depende de varios factores, entre los que se destacan la forma y densidad del objeto sumergido y la densidad del fluido.

La fuerza de flotación actúa en dirección ascendente sobre los objetos sumergidos, y varía en función de la presión; por lo tanto, a mayor profundidad, mayor será la presión en el fluido y en consecuencia, mayor será la fuerza de empuje.

Si suponemos una pecera que contiene un fluido de densidad conocida (ρ), se puede establecer que la fuerza de flotación F_F, representa la diferencia de las fuerzas ejercidas por el fluido en dos puntos que se encuentran a diferente altura:

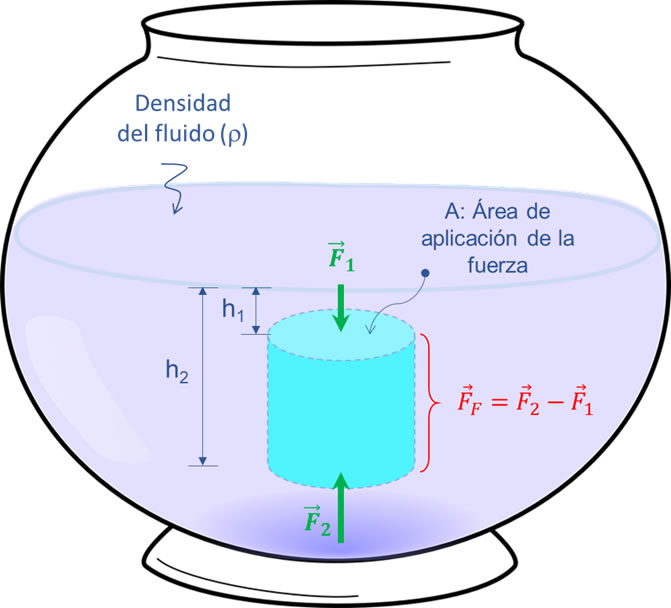
En la figura se observa las fuerzas verticales F1 y F2 debido a la presión que ejerce el fluido sobre el área superior e inferior del cilindro destacado.

En términos generales, la presión se define como la relación entre la magnitud de una fuerza y el área de la sección transversal donde actúa dicha fuerza:

\(P = \frac{F}{A}\)

Si se despeja la magnitud de la fuerza, se obtiene:

\(F = P \cdot A\)

Por otra parte, se sabe que la presión en un fluido varía linealmente con la profundidad, y se determina multiplicando la densidad del fluido por el la profundidad (h) a la cual se desea calcular la presión:

\(P = \rho \cdot h\)

Combinando las dos últimas expresiones, se obtiene:

\(F = \rho \cdot h \cdot A\)

Donde:

ρ: densidad del fluido

h: profundidad donde se mide la presión

A: área de la sección donde actúa la fuerza F

Esta ecuación, representa la magnitud de la fuerza (F) debido a la presión que ejerce un fluido sobre cualquier objeto sumergido, y su dirección es siempre perpendicular al área de contacto actuando a compresión.

En el cilindro que se muestra en la pecera, no se representan las fuerzas laterales ya que cada fuerza lateral se anula con la fuerza lateral que se encuentre en el lado opuesto del cilindro a la misma profundidad. Por el contrario, la resultante de las fuerzas verticales que se ejercen en las caras superior e inferior del cilindro no es nula ya que se encuentran a diferente profundidad, y de hecho, la diferencia de dichas fuerzas, se conoce como fuerza de flotación o de empuje (F_F).

\({\vec F_F} = {\vec F_2} – {\vec F_1} = \left( {\rho \cdot {h_2} \cdot A – \rho \cdot {h_1} \cdot A} \right)\hat j = \rho \cdot A\left( {{h_2} – {h_1}} \right)\hat j\)

Puesto que h2 > h1, la diferencia de alturas da como resultado una cantidad positiva, lo que indica que la fuerza de empuje FF es vertical hacia arriba.

Principio de Arquímedes

El principio de Arquímedes establece que la fuerza de flotación que ejerce un fluido sobre un objeto, es equivalente al peso del fluido que desplaza, por lo tanto, es una fuerza que está presente cuando los cuerpos se sumergen en fluidos ya sea de manera total o parcial.

Seguramente nos hemos preguntado alguna vez, cómo es posible que los barcos floten aun cuando están elaborados de acero, que es un material más denso que el agua, y la respuesta es que se debe a la fuerza de flotación y al hecho de que se construyen con compartimientos llenos de aire para que la densidad promedio del barco sea inferior a la del agua.

Para explicar este fenómeno, supongamos que se desea conocer el porcentaje del volumen de un barco que se hundirá en el agua, si se conoce que la densidad promedio del barco es una tercera parte de la del agua:

En primer lugar, se debe analizar el diagrama de cuerpo libre del barco como se muestra en la siguiente imagen.

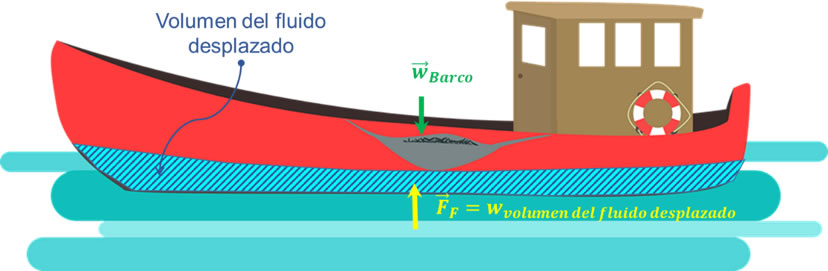
Diagrama de cuerpo libre para un barco flotando en el bar. Las fuerzas externas que actúan son el peso del barco y la fuerza de empuje.

De la segunda ley de Newton se obtiene que el peso (w) de un cuerpo es:

\(w = m \cdot g\)

Por otra parte, la densidad es:

\(\rho = \frac{m}{V}\)

Combinando estas ecuaciones, se deduce que:

\(w = \rho \cdot V \cdot g\)

Se conoce que la densidad promedio del barco es una tercera parte de la densidad del agua (ρ_barco =1/3. ρ_agua) y el volumen del barco es mayor que el volumen sumergido, por lo tanto:

\({w_{barco}} = {\rho _{barco}} \cdot {V_{Barco}} \cdot g\)

Para la condición de equilibrio en el eje vertical, se tiene:

\(\sum {F_y} = 0\)

\({F_F} – {w_{Barco}} = 0\)

De acuerdo con el principio de Arquímedes, la fuerza de empuje es equivalente al peso del volumen del fluido desplazado:

\({\rho _{Agua}} \cdot {V_{fluido\;desplazado}} \cdot g – {\rho _{barco}} \cdot {V_{Barco}} \cdot g = 0\)

\({\rho _{Agua}} \cdot {V_{fluido\;desplazado}} – \frac{1}{3} \cdot {\rho _{Agua}} \cdot {V_{Barco}} = 0\)

\({V_{fluido\;desplazado}} = \frac{1}{3} \cdot {V_{Barco}}\)

Por lo tanto,

\({V_{fluido\;desplazado}} = 30\;\% \cdot {V_{Barco}}\)

A partir de este ejemplo se puede deducir que:

• Si (ρ_objeto.V_objeto < ρ_fluido.V_fluido), el cuerpo flotará

• Si (ρ_objeto.V_objeto > ρ_fluido.V_fluido), el cuerpo se hundirá hasta el fondo

• Si (ρ_objeto.V_objeto = ρ_fluido.V_fluido), el cuerpo se sumerge pero queda en equilibrio

Los icebergs flotan gracias a que la densidad del hielo es un poco menor que la densidad del agua.

Peso aparente

El peso aparente representa el peso de un objeto que registraría un dinamómetro para un objeto que se encuentra sumergido en un fluido, ya sea de manera total o parcial. Como se muestra en la siguiente imagen, el peso aparente se encuentra en función del peso real del objeto y la fuerza de empuje que le ejerce el fluido a este.

Esto significa que se puede conocer la densidad de un objeto si se sabe su peso aparente, el peso real, el volumen y densidad del fluido desplazado.

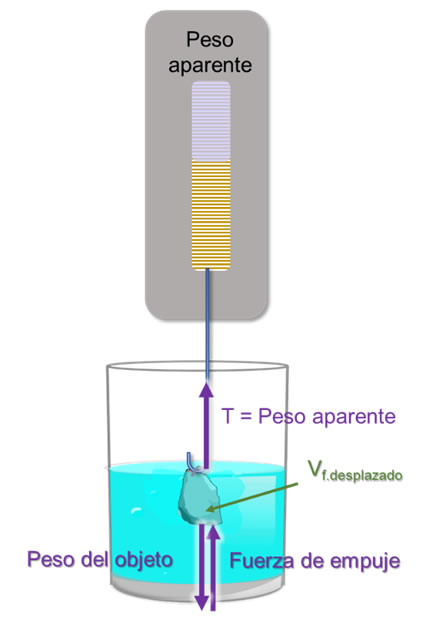
Numéricamente, el peso aparente representa la diferencia de la magnitud entre la fuerza de empuje y el peso real del objeto

Por: Evelyn Maitee Marín. Ingeniera industrial con maestría en Ciencias aplicadas de Física y doctorado en Ciencias de la Educación. Profesora de la Universidad del Zulia.

Art. actualizado: Nov. 2022; sobre el original de diciembre, 2011.

Datos para citar en modelo APA: Marín, E. M. (Nov. 2022). Definición de Flotabilidad. Significado.com. Desde https://significado.com/flotabilidad/