Definición de Elipse

Maestría en Matemáticas, Dr. en Ciencias
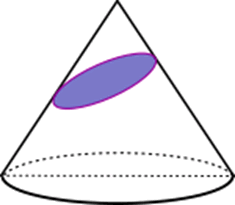
La elipse es una de las cónicas que se ha estudiado desde la época de los griegos, sobre la referencia de Apolonio, y que ha sido útil para explicar la trayectoria de los planetas y en el diseño de habitaciones con características acústicas excepcionales. Cuando un cono recto es intersectado con un plano no paralelo a la generatriz del cono ni perpendicular a su base, el resultado es una Elipse, este hecho. Cuando el plano es paralelo se forma una circunferencia y este caso merece un tratamiento especial.
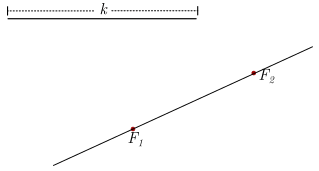
Dados dos puntos fijos \({F_1}\) y \({F_2}\), a los cuales llamaremos Focos de la Elipse y una constante \(k > 0\); la Elipse con focos en los puntos \({F_1}\) y \({F_2}\), es el lugar geométrico de los puntos en el plano cuyas distancias a los puntos \({F_1}\) y \({F_2}\) es igual a una constante \(k\), es decir:
\(P{F_1} + P{F_2} = k\)
Construcción de la elipse con regla y compás
Dados dos puntos fijos \({F_1}\) , \({F_2}\) y una constante \(k > 0\) podemos construir varios puntos que pertenezcan a la elipse que cumpla:
\(P{F_1} + P{F_2} = k;\)
Para ello es suficiente con realizar los siguientes pasos.
Situación inicial
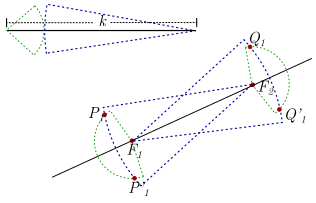
Sobre el punto \({F_1}\) se traza un arco de circunferencia de radio \({a_1}\) (verde) y sobre \({F_2}\) una circunferencia de radio \(k – {a_1}\) (azul). Se marcan las intersecciones de dichos arcos, en este caso \({P_1}\) y \(P_1^\prime\).
La manera en que se eligieron los radios se garantiza:
\({F_1}{P_1} + {F_2}{P_1} = k\)
\({F_1}P{^\prime_1} + {F_2}P{^\prime_1} = k\)
Sobre el punto \({F_2}\) se traza un arco de circunferencia de radio \({a_1}\) (verde) y sobre \({F_1}\) una circunferencia de radio \(k – {a_1}\) (azul). Se marcan las intersecciones de dichos arcos, en este caso \({Q_1}\) y \(Q_1^\prime\)
Sobre el punto \({F_1}\) se traza un arco de circunferencia de radio \({a_2}\) (verde) y sobre \({F_2}\) una circunferencia de radio \(k – {a_2}\) (azul). Se marcan las intersecciones de dichos arcos, en este caso \({P_2}\) y \(P_2^\prime\).
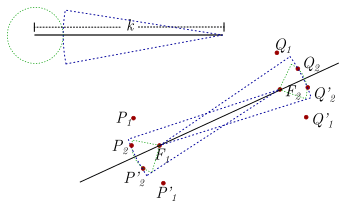
La manera en que se eligieron los radios se garantiza:
\({F_1}{P_2} + {F_2}{P_2} = k\)
\({F_1}P{^\prime_2} + {F_2}P{^\prime_3} = k\)
Sobre el punto \({F_2}\) se traza un arco de circunferencia de radio \({a_2}\) (verde) y sobre \({F_1}\) una circunferencia de radio \(k – {a_2}\) (azul). Se marcan las intersecciones de dichos arcos, en este caso \({Q_2}\) y \(Q_2^\prime\)
De manera análoga se construyen más puntos
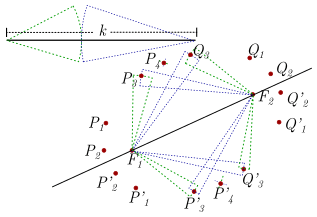
Al unir los puntos se obtiene el esbozo de una elipse cuyos focos son los puntos \({F_1}\) y \({F_2}.\)
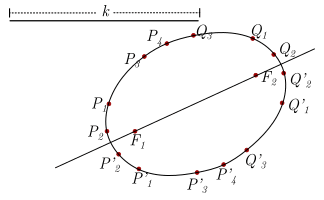
Elementos y características de la elipse
La siguiente figura muestra otros elementos importantes de la elipse.
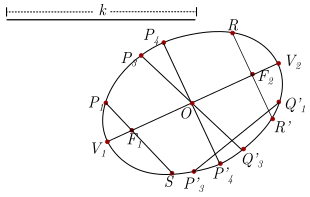
| Elemento | Descripción | Ejemplo |
|---|---|---|
| Centro de la Elipse | Punto medio del segmento \(\overline {{F_1}{F_2}} \), donde \({F_1}\) y \({F_2}\) son los focos de la elipse. | \(O\) |
| Eje Focal o eje mayor | Es la recta que pasa por los focos | |
| Vértice de la elipse | Intersección del eje focal con la elipse | \({V_1}\) y \({V_2}\) |
| Eje conjugado o eje menor | Segmento de recta que une dos puntos de la elipse | |
| Cuerda | Segmento de recta que une dos puntos de la elipse | \(\overline {P_3^\prime Q_1^\prime } \) |
| Cuerda Focal | Cuerda que pasa por uno de los focos de la elipse | \(\overline {{P_1}S} \) |
| Lado recto | Cuerda focal perpendicular al eje focal | \(\overline {RR^\prime } \) |
| Diámetro de la elipse | Cuerda que pasa por el centro | \(\overline {{P_1}P_3^\prime } \) |
Características de la elipse
La elipse tiene dos ejes de simetría a saber: el eje focal y el eje conjugado denotaremos con
\(a = O{V_1},\)\(b = OP\)\(c = O{F_1}\)
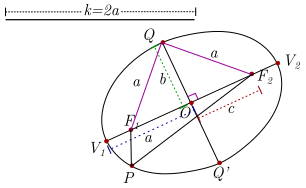
| Elemento | Descripción | Valor |
|---|---|---|
| Semi eje mayor | Longitud del segmento \(\overline {O{V_1}} \) | \(a\) |
| Semi eje menor | Longitud del segmento \(\overline {OQ} \) | \(b\) |
| Eje mayor | Longitud del segmento \(\overline {{V_1}{V_2}} \) | \(2a\) |
| Eje menor | Longitud del segmento \(\overline {QQ’} \) | \(2b\) |
| Distancia focal | Longitud del segmento \(\overline {{F_1}{F_2}} \) | 2\(c\) |
Se tienen las siguientes:
\(k = 2a\)
Es decir:
\(P{F_1} + P{F_2} = k = 2a,\;\)
Por el teorema de Pitágoras:
\({b^2} + {c^2} = {a^2}.\)
Una manera de dibujar una elipse en un programa de diseño consiste en determinar la localización del centro y los valores del eje mayor y del eje menor y no es necesario indicar la posición de cada uno de los focos de la elipse; las cuales se pueden determinar usando la relación:
\({b^2} + {c^2} = {a^2}.\)
Por ejemplo, si se traza una elipse en un programa de diseño cuyos ejes miden 6cm y 10 cm, entonces los semiejes miden 3 cm y 5cm; y la distancia focal se puede calcular de la siguiente manera:
\({3^2} + {c^2} = {5^2}\)
Al resolver la ecuación se obtiene que la distancia focal es de 4 cm.
Ecuaciones que modelan las elipses
Dados dos puntos fijos \({F_1}\) y \({F_2}\), a los cuales llamaremos Focos de la Elipse y una constante \(a > 0\); la Elipse con focos en los puntos \({F_1}\) y \({F_2}\), es el lugar geométrico de los puntos en el plano cuyas distancias a los puntos \({F_1}\) y \({F_2}\) es igual a una constante \(k\), es decir:
\(P{F_1} + P{F_2} = 2a\)
Ecuaciones de la elipse con centro en el origen y eje focal sobre uno de los ejes coordenados
Posición de la Elipse
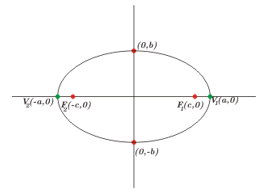
Centro en \(\left( {0,0} \right).\) Focos en \({F_1}\left( { – c,0} \right),\;{F_2}\left( {c,0} \right).\) Vértices en \({V_1}\left( { – a,0} \right),\;{V_2}\left( {a,0} \right).\;\)Eje Focal: Eje \(x\)
Ecuación de la parábola
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Donde se cumple:
\({b^2} + {c^2} = {a^2}.\)
Posición de la Elipse
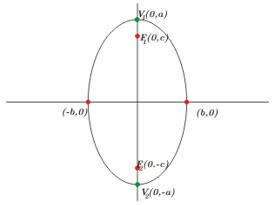
Centro en \(\left( {0,0} \right).\) Focos en \({F_1}\left( {0, – c} \right),\;{F_2}\left( {0,c} \right).\) Vértices en \({V_1}\left( {0, – a} \right),\;{V_2}\left( {0,a} \right).\;\)Eje Focal Eje \(y\)
Ecuación de la parábola
\(\frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\)
Donde se cumple:
\({b^2} + {c^2} = {a^2}\)
Ejemplos resueltos
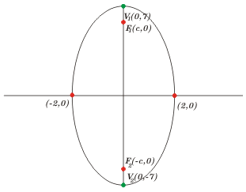
1. Características de la Elipse
El eje focal está sobre el eje de las ordenadas (eje de las \(y\)) sus semiejes miden 7 y 2 respectivamente y su centro está en el origen
Ecuación de la Elipse
En este caso
\(a = 7,\;b = 2,\) por lo tanto
\(c = \sqrt {{7^2} – {2^2}} = \sqrt {45} = \sqrt {{3^2}5} = 3\sqrt 5 \)
\(\frac{{{x^2}}}{{{b^2}}} + \frac{{{y^2}}}{{{a^2}}} = 1\)
\(\frac{{{x^2}}}{{{2^2}}} + \frac{{{y^2}}}{{{7^2}}} = 1\)
\(\frac{{{x^2}}}{4} + \frac{{{y^2}}}{{49}} = 1\)
Esbozo de la gráfica
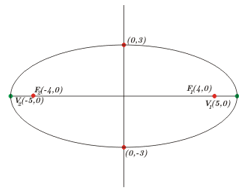
2. Características de la Elipse
El eje focal está sobre el eje de las abcisas (eje de las \(x\)), su distancia focal mide 8, su eje mayor mide 10 y centro está en el origen
Ecuación de la Elipse
En este caso
\(a = 4,\;c = 5,\) por lo tanto
\(b = \sqrt {{5^2} – {4^2}} = \sqrt 9 = 3\)
\(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
\(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
\(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
Esbozo de la gráfica
Ecuaciones sobre una elipse con la propiedad de un centro que está fuera del origen, y con un eje focal paralelo respecto de uno de los ejes coordenados
Posición de la Elipse
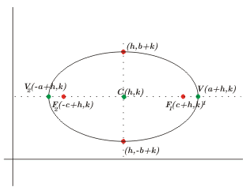
Centro en \(\left( {h,k} \right).\) Focos en \({F_1}\left( {h – c,k} \right),\;{F_2}\left( {h + c,k} \right).\) Vértices en \({V_1}\left( {h – a,k} \right),\;{V_2}\left( {h + a,k} \right).\;\)Eje Focal: \(y = k\)
Ecuación de la elipse
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
Donde se cumple:
\({b^2} + {c^2} = {a^2}.\)
Posición de la Elipse
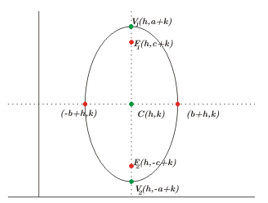
Centro en \(\left( {h,k} \right).\) Focos en \({F_1}\left( {h,k – c} \right),\;{F_2}\left( {h,k + c} \right).\) Vértices en \({V_1}\left( {h,k – a} \right),\;{V_2}\left( {h,k + a} \right).\;\)Eje Focal \(x = h\)
Ecuación de la elipse
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{b^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{a^2}}} = 1\)
Donde se cumple:
\({b^2} + {c^2} = {a^2}\)
Ejemplos resueltos
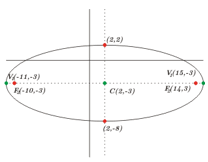
1. Características de la Elipse
Los focos son \({F_1}\left( { – 10, – 3} \right),\;{F_2}\left( {14, – 3} \right)\) y su eje mayor es igual a 26.
Ecuación de la Elipse
En este caso: \(2c = {F_1}{F_2} = 24,\) por lo tanto: \(c = 12\)
\(2a = 26\)
\(a = 13\)
\({b^2} + {c^2} = {a^2}\)
\({b^2} + {12^2} = {13^2}\)
\({b^2} = {13^2} – {12^2}\)
\({b^2} = 25\)
El centro de la elipse está en el punto medio del segmento \(\overline {{F_1}{F_2}} \) el cual es \(C\left( {2, – 3} \right).\)
El eje focal es paralelo al eje de las \(x\).
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
\(\frac{{{{\left( {x – 2} \right)}^2}}}{{{{13}^2}}} + \frac{{{{\left( {y – \left( { – 3} \right)} \right)}^2}}}{{{5^2}}} = 1\)
\(\frac{{{{\left( {x – 2} \right)}^2}}}{{25}} + \frac{{{{\left( {y + 3)} \right)}^2}}}{{169}} = 1\)
Esbozo de la gráfica
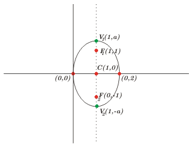
2. Características de la Elipse
Los focos son \({F_1}\left( {1,1} \right),\;{F_2}\left( {1, – 1} \right)\) y su eje menor es igual a 2.
Ecuación de la Elipse
En este caso: \(2c = {F_1}{F_2} = 2,\) por lo tanto: \(c = 1.\)
\(2b = 2\)
\(b = 1\)
\({b^2} + {c^2} = {a^2}\)
\({1^2} + {1^2} = {a^2}\)
\(2 = {a^2}\)
El centro de la elipse está en el punto medio del segmento \(\overline {{F_1}{F_2}} \) el cual es \(C\left( {1,0} \right).\)
El eje focal es paralelo al eje de las \(y\).
\(\frac{{{{\left( {x – h} \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {y – k} \right)}^2}}}{{{b^2}}} = 1\)
\(\frac{{{{\left( {x – 0} \right)}^2}}}{2} + \frac{{{{\left( {y – 1)} \right)}^2}}}{{{1^2}}} = 1\)
\(\frac{{{x^2}}}{2} + {\left( {y – 1} \right)^2} = 1\)
Esbozo de la gráfica

Art. actualizado: Nov. 2022; sobre el original de julio, 2010.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.