Definición de Ortocentro
 La palabra ortocentro es un término que se usa excluyentemente dentro del ámbito de la Geometría y refiere a aquel punto de intersección en el cual confluyen las tres altitudes de un triángulo. Es decir, en el ortocentro se cortan las tres alturas de un triángulo. Se lo simboliza a partir de la letra H mayúscula.
La palabra ortocentro es un término que se usa excluyentemente dentro del ámbito de la Geometría y refiere a aquel punto de intersección en el cual confluyen las tres altitudes de un triángulo. Es decir, en el ortocentro se cortan las tres alturas de un triángulo. Se lo simboliza a partir de la letra H mayúscula.
El triángulo, por su lado, es un polígono definido por tres rectas, las cuales se cortan dos a dos en tres puntos que no se hayan alineados; los puntos en los que se unen las rectas se llaman vértices y las porciones de recta que quedan determinadas son los lados del triángulo.
Cabe destacar que el ortocentro no resulta para nada una cuestión insignificante dado que por ejemplo tres rectas cualquiera que se toman a pares se cortarán en tres puntos distintos, en cambio, en el caso de los triángulos, las alturas se cortan en un mismo punto y eso es muy simple y sencillo de demostrar a partir de justamente el ortocentro.
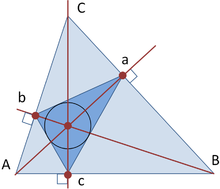
Cuando el triángulo es acutángulo, o sea, sus tres ángulos interiores son menores a 90°, el ortocentro será el incentro del triángulo órtico, que es aquel que presenta como vértices a los pies de las tres alturas, vale decir, las proyecciones de los vértices sobre sus lados. En tanto, el incentro, simbolizado a partir de la letra I, será aquel punto en el cual se intersecan las tres bisectrices de los ángulos interiores del triángulo y crea la circunferencia inscrita en el centro del triángulo en cuestión.
Por otra parte, si el triángulo es rectángulo, aquel que dispone de un ángulo recto de 90°, el ortocentro coincidirá con el vértice del mencionado ángulo recto.
Y si se trata de un triángulo obtusángulo, cuando uno de sus ángulos interiores es obtuso, o sea, mayor a 90° y los otros dos miden menos de 90°, el ortocentro se ubicará por fuera del triángulo.
Trabajo publicado en: Jun., 2012.
Escriba un comentario
Contribuya con su comentario para sumar valor, corregir o debatir el tema.Privacidad: a) sus datos no se compartirán con nadie; b) su email no será publicado; c) para evitar malos usos, todos los mensajes son moderados.